0083

Image Reconstruction with Integrated Gradient-Nonlinearity Correction and Constrained Spatial Support

Shengzhen Tao¹, Joshua D Trzasko¹, Paul T Weavers¹, Yunhong Shu¹, John Huston III¹, Erin M Gray¹, and Matt A Bernstein¹

¹Radiology, Mayo Clinic, Rochester, MN, United States

Synopsis

Due to engineering limitations, the spatial-encoding gradient fields in MRI are not exactly linear across the entire field-of-view. If not properly accounted for during reconstruction, the gradient-nonlinearity (GNL) causes image distortion and artificial signal intensity change. Conventionally, the GNL effects are corrected after image reconstruction using image-domain interpolation, followed by intensity correction using the Jacobian-determinant of the distortion field. Images corrected using this method can suffer from noise amplification at regions with strong GNL distortion. Here, we develop a model-based reconstruction method with integrated GNL correction and constrained spatial support, and demonstrate reduced noise amplification effect using this method.

Purpose

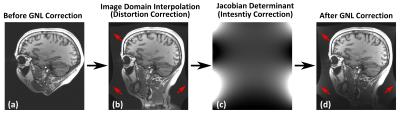
In practice, the spatial-encoding gradient fields used in conventional MRI are not exactly linear across the entire imaging volume due to various engineering limitations^1,2. If not accounted for during reconstruction, gradient-nonlinearity (GNL) causes images to be geometrically distorted^1-5. The GNL-induced distortion is conventionally corrected by interpolation after transformation to the image-domain (i.e., “GradWarp” on GE systems), followed by intensity correction approximated by the Jacobian-determinant of the distortion field¹. The intensity correction is necessary to compensate for GNL-induced image uniformity change. This method has been shown to be effective in correcting coarse image distortion on conventional whole-body MRI systems with moderate GNL⁵. However, near the peripheral regions of imaging volume where GNL-distortion is stronger, the conventional GNL correction (GNLC) can introduce noise amplification after intensity correction. This problem is especially relevant for large field-of-view imaging on whole-body scanners, and for the compact system with asymmetric gradient design⁶, whose smaller imaging volume (26-cm diameter-spherical-volume) designed for brain and extremity MRI renders the noise amplification effect to be apparent even in a brain scan FOV of 25.6cm (Figure1). Recently, we developed a model-based MRI reconstruction with integrated GNLC that prospectively accounts for GNL effect during reconstruction, rather than attempting to correct it in image domain⁷. Here, we extend this framework to include an image support constraint, and demonstrate reduced noise amplification using this method on images acquired from this compact asymmetric gradient.

Methods

Accounting for GNL, the MR signal measurement vector, $$$\bf{g}$$$, from a Cartesian acquisition assuming full k-space sampling can be modeled as:

$$\bf{g=Af+n}$$

where $$$\bf{f}$$$ denotes the image vector, $$$\bf{A}$$$ denotes the spatial-encoding operator including GNL effect with $$$\bf{A}$$$$$$(\kappa,i)=\exp(-2j\pi$$$$$$k(\kappa)\Delta$$$$$$(\bf{x}$$$$$$[i]))$$$, $$$\Delta(\bf{x})$$$ represents the GNL-induced distortion field, $$$\bf{n}$$$ denotes measured noise. For Cartesian acquisitions, $$$\bf{A}$$$ can be efficiently approximated using the type-I non-uniform-fast-Fourier-Transform (NUFFT)^7-9. Conventionally, the interpolation operator used within NUFFT assumes circulant boundary conditions. However, the GNL-induced distortion field is technically infinite and does not possess such symmetry. This discrepancy introduces numerical errors in regions with strong distortion, where image content on the opposite side can be wrapped back and interfere with other image content. To mitigate this effect, an image support constraint denoted by a binary diagonal matrix, $$$\bf{M}$$$, is introduced to mask out the regions where the distortion field violates the NUFFT boundary conditions. With this constraint, it is assumed that the image object does not occupy region outside $$$\bf{M}$$$, which is typically true for fully-sampled acquisitions on our system with conventional RF fields-of-excitation (FOX). $$$\bf{M}$$$ can be obtained based on distortion field and the size of the interpolation kernel used in NUFFT. Incorporating $$$\bf{M}$$$ into signal model leads to:

$$\bf{g=AMf+n=\begin{bmatrix}\bf{A_M}&\bf{A_0}\end{bmatrix}}\begin{bmatrix}\bf{f_M}\\\bf{0} \end{bmatrix}+\bf{n}=A_Mf_M+n$$

where $$$\bf{f_M}$$$ represents the image vector within $$$\bf{M}$$$; $$$\bf{A_M}$$$ and $$$\bf{A_0}$$$ correspond to columns in $$$\bf{A}$$$ encoding regions inside/outside $$$\bf{M}$$$. The image reconstruction can be formatted into a linear optimization:

$$\arg\min_{\bf{f_M}}\parallel\bf{g-A_{M}f_{M}}\parallel_2^2$$

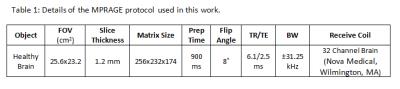
As a test, the brain of a healthy volunteer was scanned under an IRB-approved protocol on the compact 3T scanner with asymmetric transverse gradients using a MPRAGE sequence (Table1). The NUFFT operators were implemented with a 5-point Kaiser-Bessel window and an (1.25x) oversampled FFT operator^8,9. The optimization problem was solved using diagonally pre-conditioned conjugate-gradient iteration (5 iterations) with the Jacobian-determinant as a preconditioner¹⁰. Standard GNLC was also performed using cubic-spline interpolation¹. The non-iterative integrated GNLC method we previously described using adjoint-NUFFT operator and Jacobian-determinant⁷ was also performed for reference.

Results

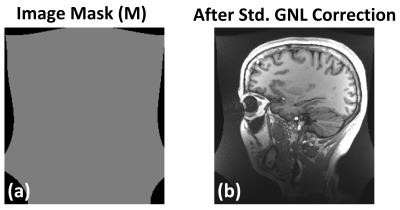
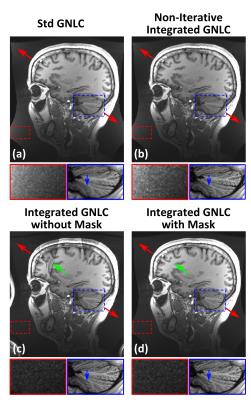
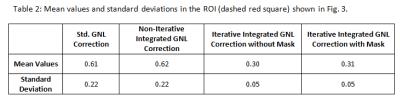
Figure2a shows an example of the image support constraint, and the corresponding image obtained after the standard GNLC (Figure2b). The black band in Figure2b is caused by missing of data required to interpolate pixel values in these regions due to GNL distortion, i.e., the interpolation kernel refers to pixel values not available in the acquired image matrix. Figure3 shows images reconstructed using the proposed iterative reconstruction without (c) and with (d) image support constraint, and images obtained after standard (a) or non-iterative integrated GNLC (b). Compared with (a/b), the proposed method (d) effectively reduces noise amplification and better preserves image details (a vs d). The use of image support constraint prevents reconstruction artifacts (green arrows). Table2 summarizes the mean values/standard deviations in selected ROI (Figure3), confirming these observations.

Discussion and Conclusion

Our results show that the proposed iterative reconstruction with integrated GNLC and constrained spatial support can alleviate the noise amplification effect observed after the standard GNLC while better preserving image details (compare Figures 3a and d). Although demonstrated on the compact asymmetric gradient with a smaller imaging volume, we expect similar noise reduction effects on a whole-body system in applications requiring large FOV (e.g.,45-50cm), such as MR-based radiation therapy planning¹¹.

Acknowledgements

This work was supported in part by the NIH grant R01EB010065.

References

1. Glover GH, Pelc NJ, inventors; General Electric Company, assignee. Method for correcting image distortion due to gradient nonuniformity. US Patent 4,591,789. May 27, 1986.

2. Harvey PR, Katznelson E. Modular gradient coil: a new concept in high-performance whole-body gradient coil design. Magn Reson Med 1999;42:561–570.

3. Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, Macfall J, Fischl B, Dale A. Reliability in multi-site structural MRI studies: Effects of gradient nonlinearity correction on phantom and human data. NeuroImage 2006;30:436–443.

4. Janke A, Zhao H, Cowin GJ, Galloway GJ, Doddrell DM. Use of spherical harmonic deconvolution methods to compensate for nonlinear gradient effects on MRI images. Magn Reson Med 2004;52:115–122.

5. Gunter JL, Bernstein MA, Borowski BJ, Ward CP, Britson PJ, Felmlee JP, Schuff N, Weiner M, Jack CR. Measurement of MRI scanner performance with the ADNI phantom. Med Phys 2009;36:2193–2205.

6. Lee SK, Mathieu JB, Graziani D, et al. Peripheral nerve stimulation characteristics of an asymmetric head-only gradient coil compatible with a high-channel-count receiver array. Magn Reson Med 2015; doi: 10.1002/mrm.26044.

7. Tao S, Trzasko JD, Shu Y, Huston J III, Bernstein MA. Integrated image reconstruction and gradient nonlinearity correction. Magn Reson Med 2015;74:1019–1031.

8. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using minmax interpolation. IEEE Trans Signal Process 2003;51:560–574.

9. Beatty PJ, Nishimura DG, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans Med Imaging 2005;24:799–808.

10. Tao S, Trzasko JD, Shu Y, Weavers PT, Huston J, Gray EM, Bernstein MA. Partial Fourier and parallel MR image reconstruction with integrated gradient nonlinearity correction. Magn Reson Med 2016;75:2534-2544.

11. Chen Z, Ma CM, Paskalev K, Li J, Yang J, Richardson T, Palacio L, Xu X, Chen L. Investigation of MR image distortion for radiotherapy treatment planning of prostate cancer. Phys Med Biol 2006;51:1393–1403.

Figures

Figure 1: Flow-chart showing the two steps in the conventional image-domain interpolation-based GNL correction. Images were acquired from a 3D-MPRAGE scan on the compact asymmetric gradient system in our institution (see texts for details). The GNL-induced distortion is first corrected using interpolation (a to b), assuming a priori known distortion field (typically obtained from electromagnetic simulation). The intensity change due to GNL was subsequently corrected using the Jacobian-determinant of the distortion field (b to d). Note the noise amplification in the peripheral of imaging volume after intensity correction (see arrows).

Figure 2: An example (a) of the image spatial support constraint (i.e., M). The gray area indicates regions where image reconstruction is performed in the proposed reconstruction method, and outside regions are assumed to have no image content. In this example, M is obtained based on the a priori known distortion field and the interpolation kernel size used in the NUFFT operator. (b): the corresponding image obtained after standard interpolation-based GNL correction. (a) and (b) have similar “black band” because of the similar interpolation kernel size used in the standard GNL correction and that used in the NUFFT (see text).

Figure 3: (a/b) Images corrected using the standard image-domain interpolation-based GNL correction (std. GNLC) and the non-iterative integrated GNLC; (c/d): images reconstructed from the proposed iterative reconstruction without (c) and with (d) image support constraint. The std. GNLC causes noise amplification around the image corners (red arrows, left zoom-in panels) and introduces image blurring after correction (blue arrows, right zoom-in panels). The non-iterative integrated GNLC (b) reduces blurring but still suffers from noise amplification as the Jacobian-determinant is used. The proposed method(d) can suppress noise amplification while preserving details. The use of image mask effectively prevents reconstruction artifacts (green arrows).

Table 1: Details of the MPRAGE protocol used in this work.

Table 2: Mean values and standard deviations in the ROI (dashed red square) shown in Fig. 3.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0083