0082
Influence of the gradient delay correction on self-navigated motion resolved reconstruction with golden angle stack-of-stars acquisitionXucheng Zhu1, Mariya Doneva2, Peder E.Z. Larson1,3, and Michael Lustig1,4
1Bioengineering, UC Berkeley-UCSF Graduate Program in Bioengineering, San Francisco, CA, United States, 2Philips Research Europe, Hamburg, Germany, 3Department of Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States, 4Department of Electrical Engineering and Computer Sciences, UC Berkeley, Berkeley, CA, United States
Synopsis
Gradient delay often leads to misalignment of k-space data, which induces artifacts on reconstructed images. As many self-gated motion correction methods largely depend on central k-space data, misalignment might affect motion state estimation and reconstruction. In order to acquire robust motion states and improve motion resolved reconstruction, we propose a workflow incorporating gradient delay correction, robust motion extraction, and motion resolved reconstruction. We tested our method on in vivo volunteer data, and demonstrate the improvement over a reconstruction that does not account for these delays.
Purpose
The 3D stack-of-stars trajectory acquisition is widely used in liver and abdominal imaging applications because of its relative insensitivity to object motion compared with Cartesian trajectory, as well as its higher acquisition efficiency compared to 3D radial trajectory. However, one drawback compared to a Cartesian acquisition is its sensitivity gradient delays. Due to this problem, the acquired k-space data might not perfectly match the designed trajectory. As self-gated motion signals are derived from the central k-space data, it would be vulnerable to the induced k-space misalignment. More importantly, gradient delays affect not only the image quality but also the accuracy of motion state estimation. Several approaches for correcting the gradient delay have been proposed in the past. One method is to measure the exact k-space location by using pre-scan or extra hardware1,2. Research5 shows that gradient delay might vary over time, some pre-calibration method might not estimate the correct delay. Another way is to calculate the delay by using acquired data3,4,9 without extra calibration. Block’s work4, used the spokes acquired at opposing orientations to estimate the gradient delay for x and y direction, then estimated delay for different direction spokes based on these two estimations. In this work, based on similar idea from Block’s work, we extended it to 3D trajectory. In addition, we estimated gradients delays for each acquisition direction instead of linear combining x and y delay components.
Methods
We assume that the gradient delay-induced k-space misalignment in the opposing orientation acquisitions were the same or similar. The correction process work flow is shown in Figure 1. Firstly, opposing orientation acquisition spokes are paired and transformed in projection domain through a Fourier transform. Then, phase differences between paired spokes are calculated and transformed back to k-space. The shift of peak from the center is the compensated phase for the paired acquisition spokes. To reduce the noise effect and error measurement, low pass filter is applied after the correction shift. An adult volunteer was scanned under IRB approval using a 3D T1-FFE sequence with a free-breathing acquisition (TR/TE 4.35 ms 1.20ms, voxel resolution 1 x 1 x 1.5mm, FOV 40 x 40 x 12.5cm). The sequence was implemented on a 3T MR system (Philips Healthcare) equipped with a 16-channel torso coil. Data processing and reconstruction steps are shown in Figure 2. Firstly, the proposed delay correction process was applied to the raw data. Then, central k-space data were selected to calculate the self-gated motion signal. After that, FLICM (fuzzy local information C-Means)7 segmentation method is used to extract the motion state curve and data are evenly binned to 4 motion states based on the curve position. Finally, motion resolved images are reconstructed by using iterative reconstruction with a total variation constraint along motion states, similar to XD-GRASP framework6 via BART (Berkeley Advanced Reconstruction Toolbox)8.
Results
Figure 3 shows the self-gated signals calculated from the raw data before and after correcting the central k-space data for gradient delay. The proposed method removes most of the intensity inhomogeneity in the self-gated signals caused by gradient delay. Then the respiration motion can be easily delineated with the proposed segmentation method with any intensity inhomogeneity correction. Figure 4 shows the motion binning signals calculated from the segmentation results based on both corrected and uncorrected data. The arrows point to errors in the binning signal due to the uncorrected gradient delay that cause a mismatch between the data and its motion state. After the gradient delay correction, the binning is largely improved. Figure 5 shows the reconstruction results with and without gradient delay correction. The proposed method improves the sharpness of the liver and some vessels inside liver because the binning process groups the motion corrupted data in the correct motion state. In addition, most of the intensity inhomogeneity and streaking artifacts caused by gradient delay are removed after the correction.
Conclusion and Discussion
In this work, we proposed a workflow to improve motion correction by correcting the gradient delay induced k-space misalignment. From the result, we found that proposed method improved both self-gated motion estimation and the overall reconstruction image quality. This workflow could also be extended to other applications using the 3D stack-of-star and conventional 2D radial trajectory.Acknowledgements
Authors would like to thank Wenwen Jiang, Jonathan Tamir, and Peng Cao for their comments and suggestions.References
[1] Peters, Dana C., J. Andrew Derbyshire, and Elliot R. McVeigh. "Centering the projection reconstruction trajectory: reducing gradient delay errors." Magnetic resonance in medicine 50.1 (2003): 1-6. [2] Speier, P., and F. Trautwein. "Robust radial imaging with predetermined isotropic gradient delay correction." Proceedings of the 14th Annual Meeting of ISMRM, Seattle, Washington, USA. 2006. [3] Block, K. T., and M. Uecker. "Simple method for adaptive gradient-delay compensation in radial MRI." Proceedings of the 19th Annual Meeting of ISMRM, Montreal, Canada. 2011. [4] Jiang, W., P.E.Z. Larson, M. Lustig. Simultaneous Estimation of Auto-calibration Data and Gradient Delays in non-Cartesian Parallel MRI using Low-rank Constraints. [5] Brodsky, Ethan K., Alexey A. Samsonov, and Walter F. Block. "Characterizing and correcting gradient errors in non-cartesian imaging: Are gradient errors linear time-invariant (LTI)?." Magnetic resonance in medicine 62.6 (2009): 1466-1476. [6] Feng, Li, et al. "XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing." Magnetic resonance in medicine 75.2 (2016): 775-788. [7] Krinidis, Stelios, and Vassilios Chatzis. "A robust fuzzy local information C-means clustering algorithm." IEEE Transactions on Image Processing 19.5 (2010): 1328-1337. [8] Uecker, Martin, et al. "Berkeley advanced reconstruction toolbox." Proc. Intl. Soc. Mag. Reson. Med. Vol. 23. 2015. [9] Wech, Tobias, et al. "Using self-consistency for an iterative trajectory adjustment (SCITA)." Magnetic resonance in medicine 73.3 (2015): 1151-1157.Figures
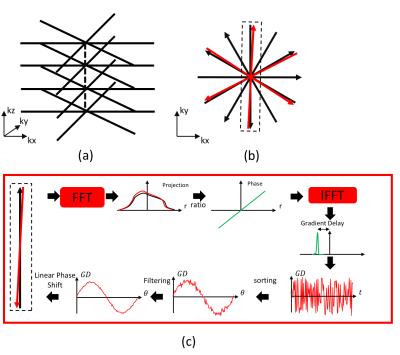
Golden angle stack-of-star trajectory is shown in (a). 3D trajectory
projected on kx-ky plane is shown in (b). Paired acquisition spokes delay
correction process is shown in (c).
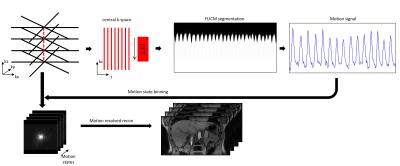
Data
processing and reconstruction steps for both corrected and non-corrected data.

Self-gated
signals are calculated by applying a Fourier transform along the kz direction
for both corrected and non-corrected data.
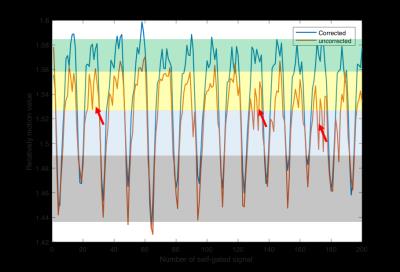
Motion
binning signals calculation based on segmenting self-navigated signal. 4 bins
are applied in this experiment.
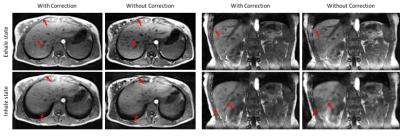
Coronal and
axial plane images of 3D motion resolved reconstruction results are compared.