0081
A New Background Field Removal Method Using Region Adaptive Kernel for Human Brain MRI1Department of Electronic Science, Xiamen University, Xiamen, People's Republic of China
Synopsis
we propose a new background field removal method by using region adaptive kernel (REAK) based on local energy distribution. Experimental results on simulation data and in vivo human data demonstrated that our method has good performance on suppressing the susceptibility artifacts caused by large susceptibility variations, such as over boundary regions of brain skull, venous vessels and paranasal sinuses. This can facilitate the susceptibility map reconstruction and achieve more accurate QSM approximate to the results of COSMOS, which is helpful for the QSM technique and its application in the clinical medicine.
INTRODUCTION
Background field removal is to separate the local field from the background field, which is a key procedure for Quantitative Susceptibility Mapping (QSM)1,2. However, there are always serious susceptibility artifacts around the regions of large susceptibility variations, e.g. the brain skull, the paranasal sinuses and major veins, which is a major challenge3,4. In this work, we propose a new background field removal method based on region adaptive kernel (REAK) according to the local energy functional.Methods
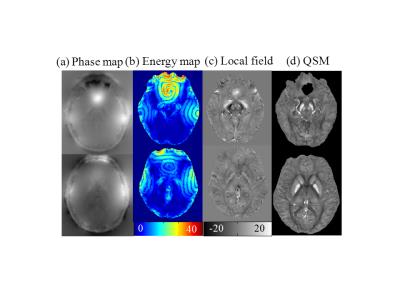
For medical MRI, intensity inhomogeneity in phase images is usually arise from the nonuniform magnetic field and variations in the tissue susceptibility. We exploit the region scalable fitting (RSF) energy functional5 to extract the field inhomogeneous information, which is formulated in a variational level set model as $$$E_{RSF}\left(\phi\right)=\sum_ \left(i=1\right)^2\alpha_{i}\int_{R_{i}}^{} K_{s}\left(x-y\right)|I\left(y\right)-f_{i}\left(x\right)|^{2}M_{i}\left(\phi\left(y\right)\right)dy+\upsilon L\left(\phi\left(x\right)\right)+\mu P\left(\phi\left(x\right)\right)$$$, where $$$\phi$$$ is the level set function and $$$M_{i}$$$ is the Heaviside function. $$$\alpha_{1}, \alpha_{2}$$$ are two positive constants and $$$\upsilon, \mu$$$ are Lagrange multipliers. The fitting functions $$$f_{1}$$$ and $$$f_{2}$$$ are $$$K_{s}$$$ weighted averages of the intensities in a neighborhood of x, while two level set regularization terms $$$L\left(\phi\right) $$$ and $$$ P\left(\phi\right)$$$ are introduced to smooth the length and preserve the regularity of the level set function. When this energy functional is minimized, the pixels of sharp field shift present high level set values. Thus, the image domain can be divided into inhomogeneous domain $$$Ω_{1}$$$ and homogeneous domain $$$Ω_{2}$$$ based on the slice averaged level set function $$$\phi_{0}$$$. In the homogeneous domain a common SMV kernel1 is used for convolution, while in the inhomogeneous domain, adaptive Spherical Gaussian Kernel (SGK) is constructed piecewise as $$$\rho_{SGK}=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{x^{2}+y^{2}+z^{2}}{2\sigma^{2}}\right)$$$ with standard deviation defined as $$$\sigma\left(X,Y,Z\right)=r\phi_{0}/C\phi\left(X,Y,Z\right)$$$, where $$$C$$$ is a constant be1.8. The kernel radius $$$r$$$ varies from 6 to 1 when the voxel location approaches to the brain boundary. Then, the local field may be obtained from the interim field data by deconvolution in Fourier domain as $$$B_i^\triangle\left(X,Y,Z\right)=\begin{cases}\left(\delta-\rho_{SGK}\right)\otimes B_{loc}\left(X,Y,Z\right), & \left(X,Y,Z\right)\in Ω_1 = \left\{\left(X,Y,Z\right)|\phi\left(X,Y,Z\right)>\phi_{0}\left(Z\right)\right\}\\\left(\delta-\rho_{SMV}\right)\otimes B_{loc}\left(X,Y,Z\right), & \left(X,Y,Z\right)\in Ω_2 = \left\{\left(X,Y,Z\right)|\phi\left(X,Y,Z\right)\leq\phi_{0}\left(Z\right)\right\}\ & \end{cases}$$$Results
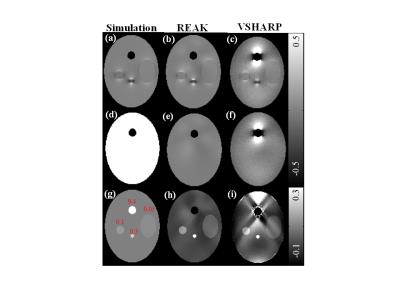
The numerical simulation data is composed of a large ellipsoid and four small spheroids to mimic the human brain tissues. A normal Gaussian noise was added setting SNR to be 40. In Fig. 2, we observe that the local field map calculated by REAK method is in better agreement with the simulated values, while the VSHARP result exhibits noticeable field bias around the ellipsoid of 9.4 ppm. Since the field error may propagate into the susceptibility reconstruction, QSM is reconstructed by SFCR method5 for further verification. We can see obvious streaking artifacts in the susceptibility map of VSHARP, but the susceptibility values corresponding to REAK are more accurate.
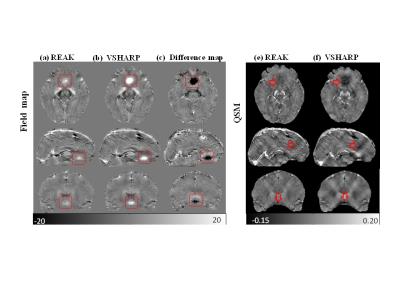
The in vivo human brain data was acquired in JHU Hospital approved by the local IRB. It was performed on a healthy male volunteer on a 7T Philips Healthcare MRI scanner with a 32-channel head coil5. In Fig. 3, there are still noticeable field perturbations of high intensities in the VSHARP result which causes strong shadow artifacts in the susceptibility map as noted with red rectangles. However, the field biases are well suppressed by REAK method and its QSM result has no obvious susceptibility artifacts and much closer to the COSMOS result. Therefore, the brain tissue structures are clearly recovered with higher contrast and more fine detail information.
Discussion
The SGK is designed as a scalable 3D Gaussian kernel whose voxel weight is adjustable depending on the local energy functional of the field perturbation. For voxels around the air-tissue boundary or strong susceptibility tissues, the SGK scale will decrease to a small size and the sphere center will be assigned with large weight, while weights of adjacent voxels decrease to zero rapidly. So field biases caused by the non-effective signal can be effectively suppressed, and then less error remains in the estimated local field map. Experimental results demonstrated that the proposed method can achieve better performance on removing the background field and facilitate the susceptibility map reconstruction.Conclusion
We propose a new background field removal method that can achieve more accurate local field estimation. In published works, paranasal sinuses are always excluded with a brain mask in QSM to suppress the strong susceptibility artifacts. However, some useful information in its neighborhood may be also precluded. Thus, we apply our method to do the background field removal with paranasal sinuses, preserving a completed brain tissues, which would be helpful in clinical applications.Acknowledgements
This work was supported in part by NNSF of China under Grant 81301277, 11375147, Doctoral Program of Higher Education of China 20130121120010 and NSF of Fujian Province of China 2014J05099, and NIH grant P41 EB015909.References
[1] Schweser F, Deistung A, Lehr B W, et al. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism?. Neuroimage, 2011, 54(4): 2789-2807.
[2] Wu B, Li W, Guidon A, et al. Whole brain susceptibility mapping using compressed sensing. Magnetic resonance in medicine, 2012, 67(1): 137-147.
[3] Sun H, Wilman A H. Background field removal using spherical mean value filtering and Tikhonov regularization. Magnetic resonance in medicine, 2014, 71(3): 1151-1157.
[4] Liu Z, Kee Y, Zhou D, Wang Y, Spincemaille P. Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping, Magnetic resonance in medicine, 2016,00:00-00.
[5] Li C, Kao C Y, Gore J C, et al. Minimization of region-scalable fitting energy for image segmentation. IEEE transactions on image processing, 2008, 17(10): 1940-1949.
[6] Bao L, Li X, Cai C, et al. Quantitative Susceptibility Mapping using Structural Feature based Collaborative Reconstruction (SFCR) in the Human Brain. 2016, 35(9): 2040-2050.
Figures