Synopsis

Concurrent field monitoring is currently limited to observation times in the order of 100 ms. However, for many purposes it is desirable to determine field dynamics continuously without interruption. To address this need we propose model-based gradient impulse response function (GIRF) harvesting, where GIRFs are continuously updated during the MR experiment. From the harvested GRIFs and the known input to the gradient chains, continuous gradients are obtained. The model-based approach allows to robustly determine continuous gradient fields with high precision. The method is demonstrated by stabilizing a gradient-demanding EPI scan.

Introduction

Magnetic field monitoring with NMR probes (1) has been used for various purposes ranging from hardware characterization to image reconstruction (2–5).

Probe signal lifetimes are currently limited to the order of 100 ms. However, for many purposes it is desirable to measure field dynamics continuously without interruption.

One option to this end is rapid alternation of multiple probe sets (6), which has been successfully pursued for assessment of sequence and hardware studies but remains to be perform concurrently with image acquisition. As an alternative, gradient prediction based on system characterization using a gradient impulse response function (GIRF) (7–9) was introduced. However, the approach does not address changes of the GIRF over time (e.g., due to thermal effects). To address this shortcoming, gradient response harvesting was recently proposed (10). The method continuously updates the gradient response from multiple short field measurements during the acquisition of the actual MR scan in conjunction with known input to the gradient chains. As discussed in reference (10), for sparse field observations, this approach yields incomplete GIRF estimates and is prone to ill-conditioning.

In this work we propose to render GIRF harvesting and continuous gradient determination more robust by incorporating system-specific GIRF models. This approach is demonstrated in an example of gradient-demanding echo-planar imaging (EPI).

Methods

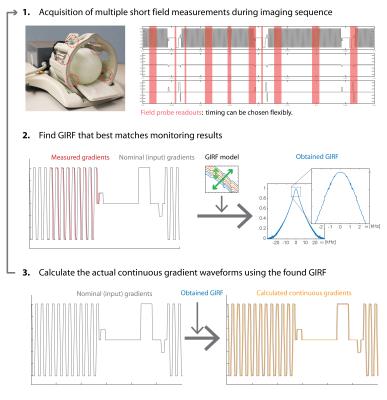
Figure 1 illustrates the basic steps of the proposed method.

Hardware and Sequences: All experiments were conducted using a 3T-Achieva MR system (Philips Healthcare). 12 ¹⁹F-based NMR field probes (8) (T2=~35ms, max. lifetime=~50ms) were mounted to a head receive coil array (Fig.1). For probe excitation and probe/coil data acquisition a dedicated RF-pulse generator and spectrometer were used. The position of the probes were obtained in an initial calibration step (1).

A gradient-demanding 2D-single-shot-EPI (resolution=1x1.5mm, TE=66ms, TR=150ms, 20 slices) with a long readout train T_acq=128ms and 150 dynamics (total duration=7:33min) was performed. During the scan, the probes were repeatedly excited (TR_probe=160ms) to monitor different parts of the sequence. From the following probe readout (max. duration=20 ms) the measured gradient output $$$o_m(t)$$$ was calculated (1) for each gradient axis.

GIRF harvesting: The GIRF relates the output of the gradient system to its input by a multiplication in the frequency ($$$\omega$$$) domain, or a convolution in the time ($$$t$$$) domain respectively:

$$\hat{o}(\omega)=\hat{i}(\omega)\cdot\hat{h}(\omega)\longleftrightarrow o(t)=i(t)*h(t)$$

A harvested GIRF that best predicts the measured gradient waveforms was obtained by minimizing $$$\sum_{t_m\in M}|o_m(t_m)-o(t_m)|$$$ for the measured time points $$$ M $$$ within each 12 seconds of the sequence by exhaustive search through the GIRF model. The GIRF model was created from a dictionary of GIRFs that were measured on different days and in various scanner states. The GIRFs were modeled by linear interpolation from a series of GIRFs that were acquired during different temperature states of the gradient coils to cover all mechanically-induced oscillatory terms. An additional exponential term, a global scaling and a time shift were added to model changes presumably from the gradient amplifier and gradient delays from various sources. To account for non-input related field drifts a field/gradient offset was added to the model.

Image reconstruction: From the obtained GIRFs and the continuous gradient channel inputs, the continuous gradient waveforms for each gradient axis were calculated and the resulting k-space trajectories (and an additionally obtained ΔB0 offset/drift) were directly used in a gridding image reconstruction without any EPI phase correction.

Results

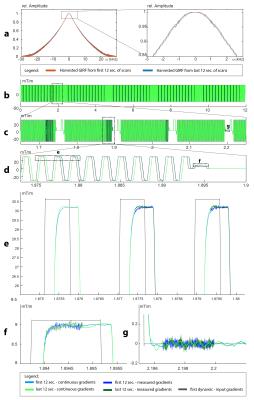
During the EPI scan, the GIRFs significantly changed (Fig.2a), which is also reflected in the obtained continuous waveforms (Fig.2b-f). Continuous and measured gradients matched accurately, indicating that harvested GIRFs are valid. In addition, the signal-to-noise ratio of the continuous waveforms is higher as compared to the measured waveforms (Fig.2e-f).

The validity of the GIRFs is also confirmed by ghosting-artifact-free images, while strong aliasing is visible when not accounting for GIRF changes (Fig.3).

Conclusion

A novel approach to obtain updated GIRFs during MR sequences was presented. The model-based method allows for the determination of complete GIRFs and includes non-input related field changes (e.g. drifts). Thereby the approach allows to robustly obtain uninterrupted gradient field waveforms with high precision.

The approach was applied for the stabilization of an EPI scan with high gradient duty-cycle to demonstrate the benefit in a demanding imaging situation. By using the harvested gradient data, all image artifacts relating to gradient encoding and changes thereof were straightforwardly corrected.

The results indicate that the method may be applied to the full range of MR experiments, which renders a routine use of this field monitoring technique possible.

Acknowledgements

References

(1) Barmet C, De Zanche N, Pruessmann KP. Spatiotemporal Magnetic Field Monitoring for MR. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med. Soc. Magn. Reson. Med. 2008;60:187–197.

(2) Wilm BJ, Barmet C, Pavan M, Pruessmann KP. Higher Order Reconstruction for MRI in the Presence of Spatiotemporal Field Perturbations. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med. Soc. Magn. Reson. Med. 2011;65:1690–1701.

(3) Kasper L, Bollmann S, Vannesjo SJ, Gross S, Haeberlin M, Dietrich BE, Pruessmann KP. Monitoring, Analysis, and Correction of Magnetic Field Fluctuations in Echo Planar Imaging Time Series. Magn. Reson. Med. 2014

(4) Vannesjo SJ, Wilm BJ, Duerst Y, Gross S, Brunner DO, Dietrich BE, Schmid T, Barmet C, Pruessmann KP. Retrospective Correction of Physiological Field Fluctuations in High-Field Brain MRI Using Concurrent Field Monitoring. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med. Soc. Magn. Reson. Med. 2014,DOI10.1002/mrm.25303.

(5) Wilm BJ, Barmet C, Gross S, Kasper L, Vannesjo SJ, Haeberlin M, Dietrich BE, Brunner DO, Schmid T, Pruessmann KP. Single-Shot Spiral Imaging Enabled by an Expanded Encoding Model: Demonstration in Diffusion MRI. Magn. Reson. Med. 2016

(6) Dietrich BE, Brunner DO, Vannesjo SJ, Wilm BJ, Pruessmann KP. Continuous 3rd-Order Field Monitoring. Proc. 23th Annu. Meet. ISMRM Tor. Can. 2015 p.:1819.

(7) Addy NO, Wu HH, Nishimura DG. A Simple Method for MR Gradient System Characterization and K-Space Trajectory Estimation. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med. Soc. Magn. Reson. Med. 2012;68:120–129.

(8) Vannesjo SJ, Haeberlin M, Kasper L, Pavan M, Wilm BJ, Barmet C, Pruessmann KP. Gradient System Characterization by Impulse Response Measurements with a Dynamic Field Camera. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med. Soc. Magn. Reson. Med. 2013;69:583–593.

(9) Campbell-Washburn AE, Xue H, Lederman RJ, Faranesh AZ, Hansen MS. Real-Time Distortion Correction of Spiral and Echo Planar Images Using the Gradient System Impulse Response Function. Magn. Reson. Med. 2015,DOI10.1002/mrm.25788.

(10) Wilm BJ, Dietrich BE, Reber J, Vannesjo SJ, Pruessmann KP. Gradient Response Harvesting for Continuous System Characterization during MR Sequences. Proc. 24th Annu. Meet. ISMRM Singapore. 2016:p. 544.