0073
Robust VFA relaxometry by Continuous Saturation of Magnetization Transfer (CSMT) effects with Non-selective Multi-Band pulses.1Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom, 2Centre for the Developing Brain, King's College London, London, United Kingdom
Synopsis
Variable Flip Angle (VFA) relaxometry methods have recently been shown to be sensitive to magnetization transfer (MT) induced bias. Common description of this effect relies on a two-pool model (restricted macromolecular pool & visible free water pool). Current practice to restrict influence of MT consists in stretching of RF pulse durations in order to minimize/counter-balance the effect of macromolecular exchange for different flip angle measurements. This work proposes to minimize the estimation bias by using constant saturation MT pulses that simultaneously excite the free-water pool and saturate the restricted-pool creating constant RF-saturation conditions independently of the flip angle (FA) applied.
Purpose
Tissue T1 and T2 are known to be dependent on measurement technique, with T1 in particular influenced by MT and the RF conditions employed1,2. For a two pool system, the observed T1 depends on the saturation state of the background pool, which is modified by the RF (B1+) pulses in the sequences applied in measurement. This effect can be quantified using [Eq.1]6 and the time structure of the measurement sequence$$<W>=\frac{\pi}{T_{RF}}\int_0^{T_{RF}}\omega_1^2(t)dt G(\Delta)=\frac{\pi}{T_{RF}}P_{RF}G(\Delta)[Eq.1]$$where TRF is the duration of the pulse, $$$\omega_1(t)=2\pi\gamma\int_0^{T_{RF}}\omega_1^{ref}(t)dt$$$is the instantaneous rotation rate caused by the pulse, $$$G(\Delta)$$$ models the absorption line-shape of the magnetization pool and PRF is the integral of $$$\omega_1^2(t)$$$. In steady-state Variable Flip Angle (VFA) methods4 a range of flip angles are deployed, creating variable saturation of the background pool within the measurement. Unless this is taken into account, the measured relaxation properties vary with the measurement parameters2,5. With this in mind, we've explored VFA T1 and T2 measurement using pulses that keep <W> constant to see if consistent saturation and hence MT conditions allow stable relaxation time measurements.
Methods
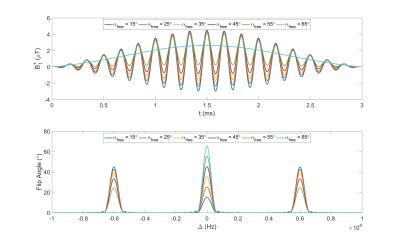
We achieve constant saturation MT (CSMT) conditions by creating a pulse that balances changes in on-resonance ($$$\Delta=0$$$) RF to achieve a required flip angle ($$$\alpha_{free}$$$) with a matched off resonance contribution to keep PRF constant. Starting with a sinc-gauss RF pulse scaled to produce a reference flip angle, $$$\alpha_{ref}=2\pi\gamma\int_0^{T_{RF}}\omega_1^{ref}(t)dt$$$, the CSMT excitation was created with symmetric bands at offset frequencies $$$\pm\Delta$$$by adding a scaled cosine modulated replica of the on-resonant pulse (Figure 1) and enforcing a relative scaling of the two components: $$\omega_1^{CSMT}(t)=2\pi\gamma[\frac{\alpha_{free}}{\alpha_{ref}}\omega_1^{ref}(t)+\kappa\omega_1^{ref}(t)\cos(\Delta.t)],$$ $$s.t.\int_0^{T{RF}}(\omega_1^{MB}(t))^2dt=\int_0^{T_{RF}}(\omega_1^{ref}(t))^2dt$$ where $$$\kappa$$$ is varied to satisfy the equal power constraint. Ideally, the background pool saturation should be independent of the balance between on- and off-resonance bands; since $$$G(\Delta)$$$ is not completely flat, $$$\Delta$$$ should be minimized, but without introducing direct on-resonant saturation of free water.Experiments were performed on three Healthy Volunteers (HV) (ages 22-58yrs) who gave informed consent. The CSMT pulse was simulated and tested with increasing PRF values of 0.86µT2ms, 3.45µT2ms, 13.81µT2ms and 55.24µT2ms on an Agarose phantom with 2%, 4% and 8% volume/volume concentrations to find combinations of TRF and that minimised direct on resonance saturation when =0, while providing efficient sequences, leading to 3ms and 6KHz respectively. Data was acquired with and : 6°,8°,10°,12°,14°,16° for SPGR and 15°,25°,35°,45°,55°,65° for SSFP with RF phase increment 180° per excitation, plus 25° and 55° for SSFP with RF phase increment 0°. To keep exchange effects between magnetization pools constant, readout (TE) and repetition (TR) times were kept constant at 3.5ms and 7ms respectively. In-vivo measurement used a sagittal geometry with 250x250x250mm3FOV, SENSE-2 for both AP and RL and acquired voxel size 0.83mm3, total time 2m13s per FA. An AFI6 map with resolution of 43mm3 was acquired to correct for spatial transmit field inhomoegeneities. For comparison, the same data was acquired using a simple scaled block pulse (TRF=0.6ms). To assess stability of the estimation with and without CSMT, multiple flip angle subsets of the acquired measurements (Table 1) were used to estimate T1 using DESPOT1 and T1,T2 using a Joint System Relaxometry (JSR) approach7 which simultaneously fits SPGR and SSFP signal models.Results
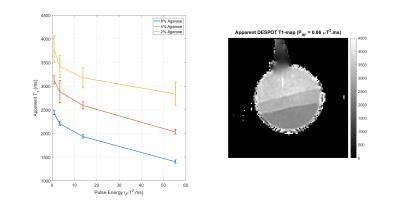
Figure 1 summarizes how apparent T1 (from DESPOT1) alters for Agarose as the PRF of the CSMT pulse is increased.
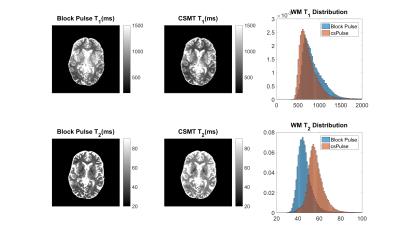
Figure 3 shows T1 (top) and T2 (bottom) maps in an exemplar axial slice using all measured data for both block pulse (left) and CSMT pulse (right).
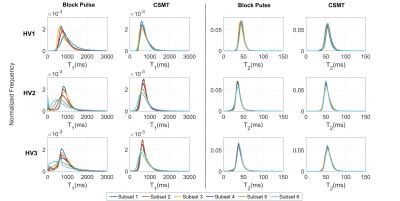
Figures 4 show histograms of T1 and T2 values from white matter for subsets 1-6 for the block and CSMT pulse, which stabilises the T1 values and results in higher T2 values, more consistent with spin echo measurements at 3T4.
Discussion & Conclusion
Relaxation times from VFA methods are influenced by RF saturation, as shown by Fig.1. Use of a constant saturation pulse results in data that is internally consistent, providing very similar relaxation time estimates when using different excitation flip angles. This is not the case when using standard block pulse excitation, as shown by Figure 4. Interestingly, not only does the CSMT approach stabilise T1, it also leads to T2 values (previously reported as underestimated using gradient echo methods2,7,9) that are more consistent with spin echo methods8. An implication is that there are no ‘ground truth’ relaxation times; instead these vary depending on saturation conditions. Explicitly acknowledging this fact could form the basis of a more traceable metrology in which MT saturation conditions are also documented. The proposed CSMT pulses may also be useful for deliberately adding MT weighting to SSFP sequences1,5 and potentially measuring z-spectra.Acknowledgements
No acknowledgement found.References
1. Bieri O. and Scheffler K. On the origin of apparent low tissue signals in balanced SSFP. Magn Reson Med. 2006; 56(5): 1067-74.
2. Yosef Al-Abasse and Gunther Helms. Influence of pulse length and shape on variable flip angle T1 mapping of the human brain. Proc. Intl. Soc. Mag. Reson. Med. 24 (2016)
3. Graham SJ, Henkelman RM. Understanding pulsed magnetization transfer. J Magn Reson Imaging 1997;7:903–912.
4. Deoni SCL, Rutt BK, Peters TM. Rapid combined T1 and T2 map- ping with gradient recalled acquisition in the steady-state. Magn Reson Med 2003; 46:515–526
5. Gloor, M, et al. Nonbalanced SSFP-based quantitative magnetization transfer imaging. Magn Reson Med 2010; 64:149–156
6. L. Yarnykh, Vasily. Actual Flip-Angle Imaging in the Pulsed Steady State: A Method for Rapid Three-Dimensional Mapping of the Transmitted Radiofrequency Field. Magn Reson Med 2007; 57:192–200
7. A. G. Teixeira Rui Pedro, J. Malik Shaihan, V. Hajnal Joseph. Joint System Relaxometry (JSR) and Crámer-Rao Lower Bound optimisation of sequence parameters: a framework for increasing precision of DESPOT T1 and T2 Estimation. Under review
8. J. Stanisz, et al. T1,T2 Relaxation and Magnetization Transfer in Tissue at 3T. Magn Reson Med. 2005; 54:507–512;
9. Crooijmans, HJA et al. Finite RF pulse correction on DESPOT2; Magn Reson Med. 2011; 65:858–862;
Figures