0067
Accelerated MR Parameter Mapping Exploiting Model-Based Simultaneous Multi-Slice Reconstruction with Hankel Subspace Learning: Application to T1 Quantification1Department of Brain and Cognitive Engineering, Korea University, Seoul, Korea, Republic of, 2Biomedical Imaging and Engineering Lab, Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Korea, Republic of
Synopsis
MR parameter mapping has been potentially of great value in diagnosing pathological diseases, but is difficult to be translated to clinical applications due to prohibitively long imaging time. It was recently shown in [1-4] that simultaneous multi-slice (SMS) imaging is highly efficient in reducing imaging time while well maintaining SNR. In this work, we propose a novel, model-based SMS reconstruction approach with Hankel subspace learning (Model-based SMS-HSL) for highly accelerated MR parameter mapping under the hypothesis that the null space in the spatial dimension, which filters out slices of no interest, is time-invariant in the parameter dimension while the dimension of temporal basis, which is found from signal evolution models, is limited.
Introduction
MR parameter mapping has been potentially of great value in diagnosing pathological diseases, but is difficult to be translated to clinical applications due to prohibitively long imaging time. It was recently shown in [1-4] that simultaneous multi-slice (SMS) imaging is highly efficient in reducing imaging time while well maintaining SNR. In this work, we propose a novel, model-based SMS reconstruction approach with Hankel subspace learning (Model-based SMS-HSL) for highly accelerated MR parameter mapping under the hypothesis that the null space in the spatial dimension, which filters out slices of no interest, is time-invariant in the parameter dimension while the dimension of temporal basis, which is found from signal evolution models, is limited. With increasing SMS factors up to 5, the proposed, model-based SMS-HSL outperforms conventional split-slice-GRAPPA in accurately estimating T1 relaxation times with relatively low artifacts and noise, potentially enabling whole-brain T1 mapping within 64sec.
Method
SMS Signal Model in k-Parameter Dimension: Since SMS signals in k-space can be represented by linear superposition of all excited slices, MR signals in k-parameter dimension is denoted in a Casorati matrix form using the Hankel operator by:
\begin{equation} \begin{split} \mathcal{H}\mathrm{\left ( \textbf{d} \right)}= {\sum_{s=1}^\mathrm{N_s}}\mathcal{H} {\left ( vec\textbf({X}_s \right )) } +\textbf{N},\;\;\;\textbf{X}_s=\begin{bmatrix} \rho_{s}(k_{1},t_{1}) & \cdots & \rho_{s}(k_{1},t_{M}) \\\vdots & \ddots & \vdots \\ \rho_{s}(k_{n},t_{1})&\cdots & \rho_{s}(k_{1},t_{M}) \end{bmatrix}\in \mathbb{C}^{\mathrm{N} \times \mathrm{M}}\end{split} \end{equation}
where, H(·) is the Hankel operator, d is the measured SMS signals in k-space, Xs is the desired k-space, s is the slice index, N is the additive noises.
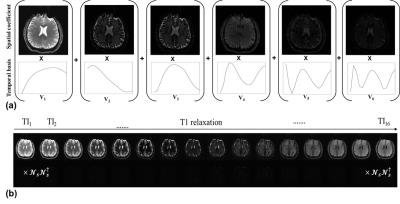
Model-Based SMS-HSL Reconstruction for T1 Mapping: It is assumed that the signal evolution of Xs along the parameter dimension follows an exponential increase by T1 relaxation times. Although the temporal signal evolution is non-linear, we hypothesize that it can be delineate by linear superposition of the temporal basis that is found by performing singular value decomposition (SVD) of the model-based simulation data. It is noted that the temporal signal variation can be synthesized using only a few principal eigenvectors in Vt. Fig. 1(a) represents the linear combination of spatial coefficient Us and corresponding temporal basis Vt. Then, slice-specific null spaces are learned by taking the right singular vectors of the composite Hankel matrix that is constructed by combining all slices other than a slice of interest from single-band calibration data [4]. Fig.1(b) Under the hypothesis that the null space in the spatial dimension, which filters out slices of no interest, is time-invariant in the parameter dimension while the dimension of temporal basis, which is found from signal evolution models, is limited, the proposed, model-based SMS-HSL reconstruction is formulated as an unconstrained optimization problem with low rank priors by exploiting that the Hankel matrix is rank-deficient and the dimension of temporal basis is finite:
$$\begin{equation} \begin{split} \label{eq:contSMSSPASE} \hat{\textbf{U}}_\mathrm{s} = \mathrm{arg} \; \underset{\textbf{U}_\mathrm{s}}{\mathrm{min}} \; \| \mathcal{H}\mathrm{\left ( \textbf{d} \right)} - {\sum_{s=1}^\mathrm{N_s}}\mathcal{H} {\left ( vec(\textbf{F}\textbf{U}_\mathrm{s}\textbf{V}_\mathrm{t} \right )) } \| + \frac{\mathrm{\lambda_L} }{2} \left \| \left ( \mathcal{H}\mathrm{\left ( \textbf{d} \right )}-\mathcal{H}\mathrm{\left ( \textbf{F}\textbf{U}_\mathrm{s}\textbf{V}_\mathrm{t} \right )} \right ) \mathrm{\mathcal{N}^c_s} \right \|_{\mathrm{F}}^{2} + \mathrm{\lambda_L} \left \| \mathcal{H}\mathrm{\left ( \textbf{F}\textbf{U}_\mathrm{s}\textbf{V}_\mathrm{t} \right )} \right \|_* \end{split} \end{equation}$$
where Us is the spatial coefficient matrix, Vt is the temporal basis, F is the spatial Fourier transform and$$$\lambda_{L}$$$ is the regularization parameter. The above optimization problem is solved by decomposing it into multiple sub-problems under the framework of variable splitting and alternating minimization methods.
Simulations and Experiments: To evaluate the feasibility of the proposed model-based SMS-HSL in highly accelerated T1 mapping, multiple sets of data were acquired using multi-point inversion recovery 2D EPI pulse sequence. Imaging parameters were: TR/TE=20000ms/27ms, FOV=220x220 mm2, matrix size=128x128, slice thickness=3mm, 16 inversion times with 34, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1200, 1400, 1600, 1800, 2000ms, and partial Fourier factor=5/8, CAIPI factors=1/5 FOV shift. With increasing SMS factors, all images were reconstructed using conventional SP-SG and model-based SMS-HSL for comparison, and parametric T1 maps were correspondingly found voxel-wise by nonlinear fitting.
Result and Discussion
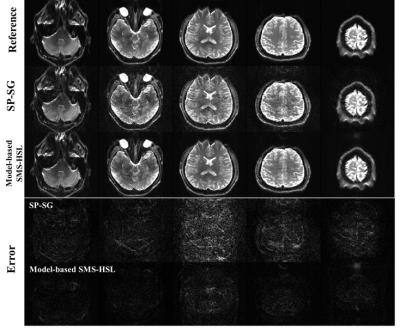
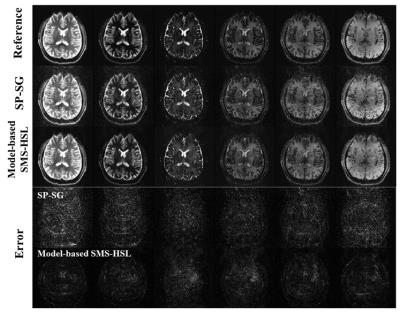
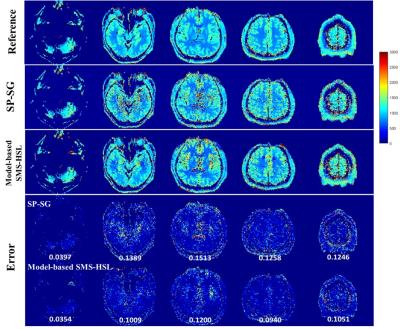
Fig. 2 demonstrates the effectiveness of proposed model-based SMS-HSL over the SP-SG in suppressing artifacts and noise at an SMS factor of 5. Fig. 3 shows reconstructed images and corresponding error maps at multiple TIs. Fig. 4 shows T1 estimates and the corresponding errors using the SP-SG and the proposed method. Compared with the SP-SG, the proposed method shows superior performance in suppressing aliasing artifacts and noises while producing accurate T1 maps.Conclusion
We successfully demonstrated that the proposed method has clear advantages over conventional method in accurately quantifying T1 maps even at high SMS factors.Acknowledgements
ICT&Future Planning (2016M3C7A1913844)
References
1. Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use ofmulticoil arrays for separation of signal from multiple slices simultaneously excited.J Magn Reson Imaging 2001; 13: 313-317.
2. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM.Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 2005; 53: 684-691.
3. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012; 67: 1210-1224.
4. Suhyung Park, Jaeseok Park. SMS-HSL: Simultaneous Multi-Slice Aliasing Separation Exploiting Hankel Subspace Learning. ISMRM 24th Annual Meeting & Exhibition, Singapore. ,0610
Figures