0066

Spherical Deconvolution of Non-Spherically Sampled Diffusion MRI Data
Jan Morez1, Jan Sijbers1, and Ben Jeurissen1

1Vision Lab, Dept. of Physics, University of Antwerp, Antwerp, Belgium

Synopsis

Multi-tissue spherical deconvolution of multi-shell diffusion MRI data allows for simultaneous estimation of the white matter fiber orientation distribution function and the apparent densities of cerebrospinal fluid and grey matter. Current spherical deconvolution approaches require that the q-space samples are distributed across shells. Here we propose a new algorithm that allows one to perform spherical deconvolution on data obtained with non-spherical sampling schemes. The algorithm is demonstrated on real data with both spherical and cartesian sampling schemes.

Purpose

Multi-tissue constrained spherical deconvolution1 (CSD) of multi-shell diffusion MRI (dMRI) data is a recently proposed technique that allows simultaneous estimation of the white matter (WM) fiber orientation distribution function (fODF) and the apparent densities of the main tissue types of the brain (cerebrospinal fluid (CSF), gray matter (GM) and WM). The current CSD approach requires the dMRI data to be distributed over shells in q-space. This limitation stems from the fact that the tissue response functions are estimated in a purely spherical manner, disregarding any radial dependencies. This precludes analysis of data acquired with non-spherical sampling schemes, e.g. Cartesian schemes used in diffusion spectrum imaging2 (DSI). In addition, multi-shell acquisition schemes might not be perfectly spherical due to gradient nonlinearities3. To address this issue, we adopt a compact model for the response function that additionally models the radial dependency of the dMRI signal and that can be evaluated at a wide range of diffusion weightings, enabling CSD for non-spherical q-space samplings.

Methods

Tissue response model for non-spherical data: We adopt a simplified 4th order tensor model to predict the dMRI signal along a range of b-values. The general expression for a 4th order tensor model is:

$$\ln S \approx \ln S_0 -b \sum _{i,j} n_i n_j D_{ij} + b^2 \sum _{i,j,k,l} n_i n_j n_k n_l W_{ijkl}$$

which we simplify to be either isotropic (in the case of CSF or GM) or axially symmetric along the z-axis (in the case of WM), similar to Jespersen et al.4 The response function parameters are estimated from sets of voxels that are deemed representative for each tissue type. Prior to estimating the WM response parameters, the gradient tables are rotated such that the principal diffusion vector coincides with the z-axis. Given the proposed parameterization, we can predict a tissue-specific dMRI signal response at arbitrary b-values. This enables us to obtain the zonal spherical harmonics (ZSH) coefficients at each individual b-value, from which the forward convolution matrix used in CSD can be constructed5. The resulting constrained linear least squares problem is identical to that of the original CSD approach:

$$ \hat{\textbf{x}} = \arg \min _{\textbf{x}} \frac{1}{2} || \textbf{Cx-y}||^2 _2 \text{ subject to } \textbf{Ax} \geq \textbf{0}$$

where $$$\hat{\textbf{x}} $$$ is the estimate of the unknown vector of coefficients of the fiber orientation distribution function (fODF), $$$\textbf{y}$$$ the vector of DW signal intensities, $$$\textbf{C}$$$ the matrix relating the coefficients of the fODF to the DW signal by means of spherical convolution and $$$\textbf{A}$$$ the constraint matrix.

Acquisition: The proposed method was tested on two data sets:

1) A multi-shell data set with isotropic resolution of 2.4mm and $$$b$$$-values 0, 700, 1200 and 2800 $$$s/mm^2$$$, with 8, 25, 45 and 75 directions per shell, respectively.

2) A DSI data set obtained from the MASSIVE database6 (DSI8-PA-pos) with isotropic resolution of 2.5mm, with $$$b$$$-values ranging from 0 to 9000$$$s/mm^2$$$ and 365 q-space samples on a Cartesian grid.

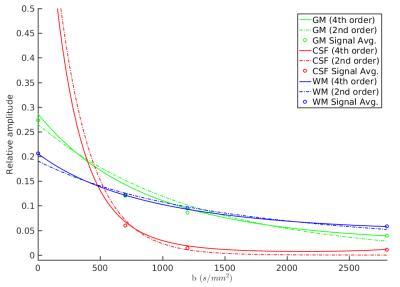
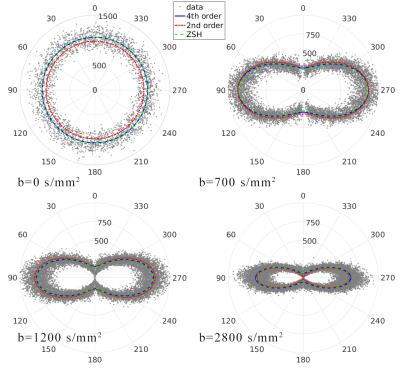
Experiments: The multi-shell data set was processed using the traditional shell-based response function estimation using a ZSH model, as well as the proposed response function estimation using the simplified 4th order tensor model. For reference, we also provide response functions estimated using a simplified 2nd order tensor model.The DSI data set was processed only using the simplified tensor models as its non-spherical nature precluded analysis with the traditional CSD approach.

Results

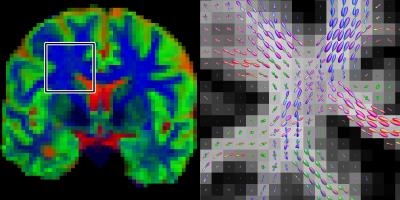
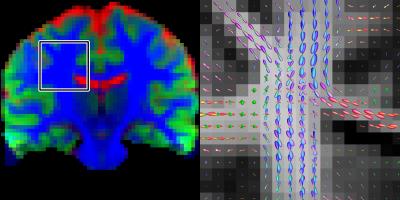
Figure 1 shows the different tissue response function models fitted to the multi-shell data. Both the 4th order and ZSH models show good correspondence with the average signal for the entire range of b-values. The 2nd order model fails over the entire range of b-values (see fig. 2 as well). Figure 2 shows the angular response function models of WM for increasing b-values. Figure 3 shows the apparent tissue volume fraction maps (left) and the fODFs (right) obtained from the spherically sampled data. Nearly identical results are obtained using the conventional ZSH responses (result not shown). Figure 4 is analogous to 3 but with a Cartesian sampling scheme.

Discussion & Conclusion

A simplified 4th order tensor model was demonstrated to provide a good fit to the tissue response signals across multiple shells, as opposed to the more commonly used 2nd order tensor model. On data with spherical q-space sampling, the estimated tissue responses and the corresponding fODFs strongly agree with those obtained with the current shell-based ZSH approach. Using a data set with Cartesian q-space sampling, we have demonstrated the feasibility of (multi-tissue) CSD on data sets with non-spherical sampling. Our approach significantly broadens the range of data sets that can be processed using CSD.

Acknowledgements

This work was supported by BELSPO Prodex (project: BRAIN-DTI). BJ is a postdoctoral fellow supported by FWO-Vlaanderen.

References

1. Jeurissen B., Tournier J.D., Dhollander T., Connelly A., Sijbers J., Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data, NeuroImage (2014), 103: Pages 411-426

2. Wedeen V. J., Hagmann. P., Tseng. W.-Y. I., Reese T. G. and Weisskoff R. M., Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med. (2005), 54: 1377–1386

3. Glasser M.F., Sotiropoulos S.N., Wilson J.A., et al., The Minimal Preprocessing Pipelines for the Human Connectome Project. NeuroImage (2013), 80: 105-124

4. Hansen B., Shemesh N., & Jespersen S. N. (2016). Fast imaging of mean, axial and radial diffusion kurtosis. NeuroImage (2016), 142: 381–393

5. Tournier J.D., Calamante F., Connelly A., Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution, NeuroImage (2007), 35: 1459-1472

6. Froeling M., Tax C.M.W., Vos S. B., Luijten P. R. and Leemans A., “MASSIVE” Brain Dataset: Multiple Acquisitions for Standardization of Structural Imaging Validation and Evaluation. Magn. Reson. Med. (2016), doi:10.1002/mrm.26259

Figures

Figure 1: Relative response function amplitudes (curves) predicted by the different models estimated from spherically sampled data, and signal averages per b-shell (circles). The CSF curve crosses the $$$y$$$-axis at $$$y=1$$$ (not shown). The 4th order model more closely predicts the dMRI signal across b-values.

Figure 2: dMRI signal amplitudes as a function of gradient orientation for the single fiber WM voxels (grey dots) and the corresponding model fits. The 4th order tensor model corresponds well with the ZSH fit.

Figure 3: Volume fraction map (left) for CSF, GM and WM (resp. red, green and blue) and fODFs (right) obtained using multi-tissue CSD from the data with a spherical sampling scheme and using the proposed 4th order tensor models for the tissue responses.

Figure 4: Volume fraction map (left) for CSF, GM and WM (resp. red, green and blue) and fODFs (right) obtained using multi-tissue CSD from the data with a Cartesian sampling scheme and using the proposed 4th order tensor models for the tissue responses.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0066