Introduction

Due to the limited resolution of DWI data, tractography streamlines merely represent sample pathways through a voxelwise tensor field, and cannot alone directly represent individual axons. Recent work¹ has proposed the use of short streamlines - streamlets - for the visualisation of potential tractography pathways, with the goal of breaking the potentially problematic perceptual association between the true anatomical brain fibres and the fibre-like streamlines. Here we extend this work beyond visualisation and propose a framework for performing tractography using streamlets. We show how conventional tractographic analysis can be readily achieved to assess connectivity between brain regions, and discuss the benefits of the new approach over conventional methods.

Methods

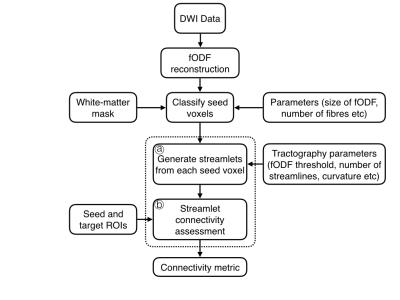
The proposed framework for streamlet tractography is presented in Figure 1. The primary difference is the subdivision of streamlining into two sub-steps: (a) generation of streamlets and (b) assessment of connectivity between streamlets. The prior and subsequent steps remain identical to conventional tractography pipelines: DWI data is first preprocessed and voxelwise reconstructions of ODFs or fODFs are then generated; finally, the brain connectivity patterns between regions is assessed using, for example, graph-based analysis. Just as for their use in visualisation, the generation of streamlets for tractography is flexible and offers the possibility to parametrically control tractography, both according to location and as directed by the data. For example, whilst the DWI data provides strong estimates of the fODFs, then a streamlet may be permitted to continue propagating. However, data that is unable to provide confident estimates of fibre direction would cause a streamlet to halt. In this case, the length of the resultant streamlets thereby represents the local confidence of the tractography, however other configurations are envisaged. As in conventional tractography, additional constraints to the propagation of streamlets, such as maximum-permitted curvature, can also be applied. As the streamlets are by design considerably shorter than conventional streamlines, they only represent an approximation to local connectivity and cannot be directly used for structural connectivity. Instead, a subsequent step must collate the ‘flows’ of streamlets together to assess region-to-region connectivity. Here we present two ideas for achieving this: mathematical morphology², and persistent homology³. The former is a standard image processing technique performed in voxelspace, which grows the individual units (here, streamlets) into large, connected components. Connectivity between seed and target regions is then achieved by testing their overlap with the resultant connected component. Mathematical morphology is challenged by the need to resample the streamlets onto a suitable voxelgrid. However, the same principles can also be achieved by applying a branch of algebraic topology called persistent homology directly to the streamlets in $$${\mathbf R}^3$$$. By considering each streamlet to be a simplicial complex (specifically a 1-simplex), it is possible to compute the connectivity between sets of streamlets by evaluation of the Cech complex for a ranges of values. Subsequent calculation of the zero’th Betti number provides an equivalent of calculating whether a set of objects in voxelspace are conjoined.

Results

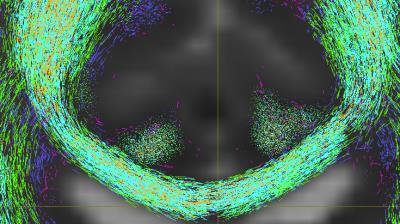
An example of streamlets generated on a single subject from the Human Connectome Project (HCP)⁴ is shown in Figure 2 (5 streamlets randomly seeded within each WM voxel). Here the different colours represent different sets of streamlets, each initiated within and propagated through voxels which matched differing fODF thresholds. The fODFs were calculated using CSD (standard default parameters) in MRtrix⁵. Figure 3 shows the result of mathematical morphological dilation and segregation into connected components on the same data in Figure 2. Here the streamlet data was first resampled onto a fine grid (0.05mm isotropic) using MRtrix, before undergoing morphological dilation (disk, radius 1) in Matlab, and finally automatic segregation into independent connected components (represented as separate colours). The segmentation correctly separates the merged streamlets along known fibre bundles.

Discussion and Conclusion

The proposed streamlet tractography framework provides an alternative to conventional streamline tractography, and combines the advantages of both streamline and global methods. The inclusion of a multistep procedure offers several advantages. Firstly, it separates the streamlining and connectivity steps, which permits each to be optimised to their own purpose. For example, this avoids the need to adapt the streamlining algorithm to account for curvature or achieve distal (from the seed) propagation through complex areas. Second, because it includes a method for groupwise aggregation of local tractographic data, it permits the local adaptation of the streamlining according to prior or alternative data, e.g. by including streamlets from prior experiments. Whilst this flexibility comes with the cost of yet more tractography parameters, the potential improvements could prove beneficial in overcoming some of the biases that still challenge tractography.

Acknowledgements

No acknowledgement found.