0064
Toward interrogating relationships between grey and white matter measures using Fixel Track-Weighted Imaging and Fixel-Based Analysis1The Florey Institute of Neuroscience and Mental Health, Heidelberg, Australia, 2Department of Neurology, Austin Health, Melbourne, Australia, 3Department of Medicine (AH/NH), The University of Melbourne, Australia
Synopsis
Neuroimaging studies assessing white and grey matter are most typically performed as independent analyses. The relationships between white and grey matter abnormalities are therefore poorly understood. We present a novel framework for interrogating relationships between quantitative measures derived from grey matter analysis, and diffusion MRI-based, fibre-specific white matter measures.
Introduction
Quantitative measures estimated from neuroimaging typically focus on either grey or white matter. As such, these measures are analysed using techniques specifically tailored for the biological tissue of interest. This however limits the extent to which grey and white matter measures may be analysed in combination, despite their intrinsic relationship via neuronal connectivity. Here we propose a framework for combining such measures into a common space, by using updates to the Track-Weighted Imaging (TWI) framework[1] to project grey matter measures into the white matter based on streamlines tractography, thereby working toward statistical analysis of these data in conjunction with quantitative and fibre-specific measures / methods designed specifically for white matter analysis in the presence of crossing fibres[2].Methods
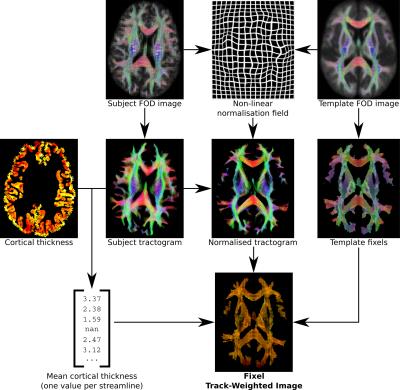
The proposed framework operates as follows (Figure 1):
1. White matter analysis:
1.1. Generate whole-brain tractogram in native subject space (rather than using warped images in template space[3]).
1.2. Perform image registration to a common template space, ideally based on a higher-order diffusion model[4].
1.3. Define the target fixels (specific fibre population elements within voxels)[5] for this analysis in template space.
2. Grey matter analysis:
2.1. For each streamline in the tractogram, sample the grey matter parameter(s) of interest at the two streamline endpoints; either using a native surface mesh representation, simply sampling at the streamline endpoints e.g.[6], or 'extending' the streamline endpoints to sample from grey matter e.g.[7].
2.2. Typically take some statistic of the two endpoint values (e.g. mean) as the 'TWI factor' for that streamline.
2.3. Transform subject tractogram to template space based on the non-linear displacement field derived during symmetric registration. Unlike FOD-based spatial normalisation, where modulation of fibre density based on fibre orientation must be performed explicitly[2], this approach implicitly modulates streamlines density appropriately depending on their orientation relative to field deformations (Figure 2)[2].
2.4. Perform Fixel Track-Weighted Imaging (TWI), with per-streamline factors defined in step 2.2, and fixels defined in group average template space in step 1.3 acting as the targets for streamlines mapping (common across all subjects).
Demonstration data
Data for 28 healthy controls were acquired on a Siemens 3T Trio system. Image data used included T1-weighted image at 0.9mm isotropic resolution, DWI (b=3000 s.mm-2, 60 directions, 2.5mm isotropic), and a pair of b=0 images with reversed phase encoding for field inhomogeneity estimation[8].
Subject-specific reconstruction included: Cortical thickness estimation using FreeSurfer[9]; Fibre Orientation Distributions estimated using Multi-Tissue Constrained Spherical Deconvolution[10]; tractogram reconstruction using the iFOD2 probabilistic streamlines algorithm[11] and the Anatomically-Constrained Tractography framework[12]; quantitative streamline weights derived using the SIFT2 algorithm[13].
A population-specific Fibre Orientation Distribution (FOD) template image was constructed using previously described methods[2,4].
For demonstration purposes, for each streamline, the mean cortical thickness at the streamline endpoints (using only one endpoint if the other did not terminate at the cortex) was used as the TWI factor for that streamline. During mapping, the mean TWI factor for streamlines traversing a particular fixel in template space was taken as the final value for that fixel.
The white matter quantitative value of interest for this demonstration was the combined measure of Fibre Density and Cross-sectional area (FDC)[2] throughout the template fixel mask.
Results
Figure 3 demonstrates how the proposed framework provides both white and grey matter quantitative measures in a common space: that of fixels in a group average WM template. An example zoomed view of this information is presented in Figure 4.Discussion
By drawing grey matter quantitative information directly into the space in which white matter quantitative measures are analysed, the measures become directly comparable in this higher-dimensional space, without the loss of complex white matter fibre crossing information. Although this process may result in grey matter information that is 'smooth' along the relevant white matter pathway, such smoothness is a preferable trait, and in fact smoothing is typically applied explicitly[7].
Future developments to the Fixel-Based Analysis (FBA) framework[2] will enable direct multivariate statistical analysis of data such as that shown. Connectivity-based Fixel Enhancement (CFE)[5] will be used for hypothesis testing in template space, incorporating both grey and white matter quantitative measures. Combined with the flexibility of the Track-Weighted Imaging (TWI) framework[1] (particularly mapping to target fixels as presented here), and the General Linear Model (GLM) with permutation testing[14], this framework will enable hypothesis formation and testing where (any) quantitative measures from both white and grey matter are of interest.
Examining relationships between such measures has the potential for improved sensitivity to neurological diseases, compared to assessing the grey or white matter alone.
Acknowledgements
We are grateful to the National Health and Medical Research Council (NHMRC) (400121) of Australia and the Victorian Government’s Operational Infrastructure Support Program for their support.References
1. Calamante, F.; Tournier, J.-D.; Smith, R. E. & Connelly, A. A generalised framework for super-resolution track-weighted imaging. NeuroImage, 2012, 59, 2494-2503
2. Raffelt, D. A.; Tournier, J.-D.; Smith, R. E.; Vaughan, D. N.; Jackson, G.; Ridgway, G. R. & Connelly, A. Investigating white matter fibre density and morphology using fixel-based analysis. NeuroImage, 2016, j.neuroimage.2016.09.029
3. Christiaens, D.; Dhollander, T.; Maes, F.; Sunaert, S. & Suetens, P. The Effect of Reorientation of the Fibre Orientation Distribution on Fibre Tracking. Computational Diffusion MRI, 2012
4. Raffelt, D.; Tournier, J.-D.; Fripp, J.; Crozier, S.; Connelly, A. & Salvado, O. Symmetric diffeomorphic registration of fibre orientation distributions. NeuroImage, 2011, 56, 1171-1180
5. Raffelt, D. A.; Smith, R. E.; Ridgway, G. R.; Tournier, J.-D.; Vaughan, D. N.; Rose, S.; Henderson, R. & Connelly, A. Connectivity-based fixel enhancement: Whole-brain statistical analysis of diffusion MRI measures in the presence of crossing fibres. NeuroImage, 2015, 117, 40-55
6. Calamante, F.; Smith, R.E.; Liang, X.; Zalesky, A.; Connelly, A. Track-weighted dynamic functional connectivity (TWdFC): a new method to study dynamic connectivity. In Proc ISMRM 2016:0308
7. Tozer, D.; Chard, D.; Bodini, B.; Ciccarelli, O.; Miller, D.; Thompson, A. & Wheeler-Kingshott, C. Linking white matter tracts to associated cortical grey matter: A tract extension methodology. NeuroImage, 2012, 59, 3094-3102
8. Andersson, J. L.; Skare, S. & Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage, 2003, 20, 870-888
9. Dale, A. M.; Fischl, B. & Sereno, M. I. Cortical Surface-Based Analysis: I. Segmentation and Surface Reconstruction. NeuroImage, 1999, 9, 179-194
10. Dhollander, T.; Connelly, A. A Novel Iterative Approach to Reap the Benefits of Multi-Tissue CSD from Just Single-Shell (+b=0) Diffusion MRI Data. In Proc ISMRM, 2016, 3010
11. Tournier, J.-D.; Calamante, F. & Connelly, A. Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions. In proc ISMRM, 2010, 1670
12. Smith, R. E.; Tournier, J.-D.; Calamante, F. & Connelly, A. Anatomically-constrained tractography: Improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage, 2012, 62, 1924-1938
13. Smith, R. E.; Tournier, J.-D.; Calamante, F. & Connelly, A. SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. NeuroImage, 2015, 119, 338-351
14. Winkler, A. M.; Ridgway, G. R.; Webster, M. A.; Smith, S. M. & Nichols, T. E. Permutation inference for the general linear model. NeuroImage, 2014, 92, 381-397
Figures