0003
Modeling of Peripheral Nervous Stimulation Thresholds in Realistic Body ModelsMathias Davids1,2, Bastien Guérin2,3, Lothar R Schad1, and Lawrence L Wald2,3,4
1Computer Assisted Clinical Medicine, Heidelberg University, Mannheim, Germany, 2Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Harvard-MIT Division of Health Sciences Technology, Cambridge, United States
Synopsis
Peripheral Nervous Stimulation (PNS) has become an important limitation in MRI with the latest generation of high-performance gradient systems. We present – to our knowledge for the first time – a model to predict PNS thresholds for arbitrary coil geometries. Our model consists of an accurate body model for EM simulations, a detailed nerve atlas of the human body, and a numerical model to predict nerve responses to induced electrical fields. With this model, we were able to reproduce PNS threshold curves of two leg/arm solenoid coils that were previously evaluated experimentally. We intent to use this PNS model to design high-performance gradient coils with significantly lowered PNS capabilities.
Target audience:
MRI gradient designers, MR safety researchersPurpose:
Peripheral Nerve Stimulation (PNS) has become the main constraint for fast imaging with MRI and MPI as other engineering barriers to high gradient strength and slew rate have been solved in the latest generation of 80 - 300 mT/m gradients with slew rates of 200 T/m/s [1,2]. Rapid switching of MRI gradients or MPI coils induces electrical fields in the human body powerful enough to cause nerve stimulation. PNS thresholds are usually characterized as the smallest field strength ΔB or gradient amplitude that initiates PNS for a sinusoidal waveform at a given frequency. A related measure is the smallest field strength/gradient amplitude for a given rise-time in an applied trapezoidal waveform. These curves are typically obtained experimentally and very little work has been done on numerical simulation of PNS induced by realistic coils in MPI and MRI [3]. We present – to our knowledge for the first time – a whole body PNS model to predict PNS thresholds for arbitrary coil designs and localize the site of stimulation [4], thus allowing optimization of MRI gradient hardware without the need to build expensive prototypesMethods:
Our model has three components (Figure 1): A) a whole body model used in electromagnetic (EM) field simulations, B) a detailed nerve atlas of the human body, C) a numerical framework to model the nerve dynamics in presence of external E-fields. Body Model: We generated a body model (tetrahedral mesh) based on anatomical surface data, including bones, muscle, brain/spinal cord, and skin. The tissue data was discretized to create a voxel model (1mm resolution), which we complemented by the lungs and the intestinal tract by using morphological operations to fill the chest and abdominal regions. The remaining unspecified voxels where defined as fatty tissue. The final voxel model was remeshed using CGAL [5] and post-processed to generate watertight 2-manifold meshes without surface intersections for each tissue. These meshes can be processed by CST (Darmstadt, Germany) or other EM field simulation platforms. EM Simulation: We simulated two solenoid coils [6] (leg coil with 54 turns, arm coil with 72 turns) for which PNS thresholds were previously obtained in volunteer experiments. The coils were modeled in CST using current paths (conductive paths with zero diameter). We used CST’s LF frequency domain solver to compute the EM fields in the body model. Electromagnetic tissue properties were taken from the Gabriel database [7]. Nerve Atlas: Based on the mesh model of the nerves, we computed centerlines of the nerves and performed a network analysis to generate a graph representation of the nerve tree. Each nerve track was assigned connectivity properties (“parent” and “children” nerves) and a fiber diameter (note that the fiber diameter has a big impact on the threshold for action potential generation, Figure 2). We then interpolated and integrated the E-fields along the nerves to obtain the external electrical potentials, which we used as inputs to the never membrane model. Nerve Membrane Model: The electrical potentials along the nerves were modulated by a driving waveform (sinusoidal waveform for MPI, sinusoidal/trapezoidal waveforms for MRI), fed into a nerve membrane model (MRG model, [8]), and evaluated using the NEURON environment [9]. The MRG model consists of a double cable electrical circuit, with explicit representation of the myelin insulation, the axon, and the nodes of Ranvier (see Figure 1, C). It was used to simulate the nerve responses to the time-varying E-fields induced by the coil, including generation of action potentials. Evaluation: For the two solenoid coils, the E-fields were modulated at a range of frequencies (460 Hz to 10.5 kHz). The strength was increased until an action potential was generated (PNS threshold).Results:
Figure 3 summarizes the PNS simulation results of the arm and leg solenoid coils, including the simulation setup, showing the coil windings, the anatomy (only the skeleton is shown for clarity), and a sagittal view of the E-field distribution. Figure 3 B and 3 D show the simulated PNS thresholds superimposed to the measurement data. There is good overall agreement between simulated and measured thresholds. The remaining deviations from the measured PNS thresholds are likely due to deviations between our anatomical model and the experimental subject’s anatomy and inaccuracies in the nerve membrane model. We believe that these preliminary results show the feasibility of using complex anatomical models in combination with nerve membrane models to estimate PNS limits for specific coil geometries. We intend to use this PNS model for numerical optimization of MPI and MRI gradient coils with significantly lowered PNS capabilities.Acknowledgements
No acknowledgement found.References
[1] McNab et al., NeuroImage 80, 2013; [2] Setsompop et al., NeuroImage 80, 2013; [3] Neufeld et al., Phys. Med. Biol. 61(12), 2016; [4] Davids et al., WMIC 2016, New York, USA, p. 557; [5] CGAL, Computational Geometry Algorithms Library, http://www.cgal.org; [6] Saritas et al., IEEE TMI, 32(9), 2013; [7] Gabriel, Radiofrequency Radiation Division, Brooks Air Force Base, Texas, 1996; [8] MyIntyre et al., J Neurophysiol. 87(2); [9] Carnevale et al., The NEURON Book, Cambridge University Press, 2006Figures
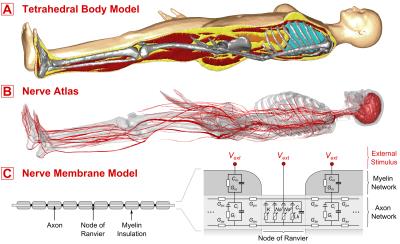
Figure 1: Components of our PNS model, A) Tetrahedral body model to compute E-fields induced by different coils, B) Nerve Atlas that encodes locations and excitability properties of major nerve fibers in the human body. The E-fields are sampled along these fibers. C) A Nerve Membrane Model is used to simulate the nerves response to external time-varying electrical fields, including possible action potentials.
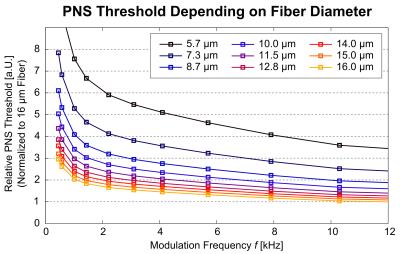
Figure 2: PNS
thresholds as a function of the modulation frequency, shown for varying
diameters of the nerve fiber (5.7 μm to 16 μm). The largest fiber (16 μm,
yellow) exhibits the smallest PNS threshold and, therefore, can be stimulated
most easily by externally applied E-fields. The PNS thresholds of the smallest
fiber (5.7 μm, black) are about a factor of 3.5 higher than the thresholds of
the 16 μm.
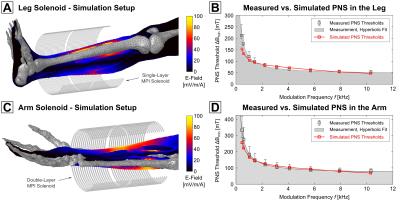
Figure 3: We
simulated PNS thresholds of two coils, a leg solenoid (A) and an arm solenoid (C);
for each setup the coil windings, the skeleton anatomy, and a sagittal slice of
the E-field distribution are shown (simulated at 1 kHz, 1 A driving current).
There is good overall agreement of the simulated threshold curves shown in (B and D, red curve) and the measured thresholds (grey).