4905

Gradient echo modelling with macroscopic field variations and large flip angles

Martin Soellradl¹, Stefan Ropele¹, and Christian Langkammer¹

¹Department of Neurology, Medical University of Graz, Graz, Austria

Synopsis

The signal decay of a 2D gradient echo sequence is substantially influenced by macroscopic field variations along the slice profile. Here we propose a numerical model describing the signal decay due to a macroscopic field gradient for arbitrary excitation pulses with large flip angles. Phantom and in-vivo experiments show that accurate modelling requires inclusion of the phase along the slice profile and the polarity of the slice selection gradient. Additionally, we show that applying the model yields better results for R₂^*-mapping and myelin water fraction estimation.

Introduction

In the presence of a varying macroscopic field Δω(z), intravoxel dephasing along the slice profile yields an overestimated effective transverse relaxation rate R₂^*^1–6. Based on the Fourier approximation of the slice profile an accurate modeling for gradient echoes with flip angles α<60° was presented in³. Here, we investigated the signal behavior for α>60° for applications that require long TR and thus larger α and propose a numerical model for arbitrary excitation pulses with linear approximated Δω(z).

We show that for a proper modeling the polarity of the slice selection gradient G_slice and the phase along the slice profile have to be considered and demonstrate that not only R₂^*-mapping but also clinical interesting applications such as whole brain myelin water fraction (MWF) imaging can be substantially improved with the proposed model.

Methods

In a 2D gradient echo sequence the measured signal at time t for slice position z_i in slice selection direction z is described by:

$$S(z_{i}, t)=\int_{-\infty}^\infty|M_{xy}(z-z_i)|~e^{i\phi_{xy}(z-z_i)}~e^{i\gamma\Delta \omega(z)t}~ e^{i\phi_0(z)}~dz~S_{model}(t)$$

where |M_xy(z- z_i )| is the magnitude and φ_xy(z- z_i) the phase of transverse magnetization, φ₀(z) the phase offset and S_model(t) the signal model. Rewriting Equation (1) by introducing F(z_i,t), which describes all components causing additional dephasing to S_model(t), leads to⁵:

$$S(z_{i}, t)=~S_{model}(t)~F(z_i,t)$$

Numerical model F(z_i,t): |M_xy(z)| and φ_xy(z- z_i) for the RF-pulse envelope B₁(t) were estimated with a numerical Bloch solver⁷. To account for B₁⁺ field variations, B₁(t) was multiplied with values obtained from B₁-map.To model variations of the slice profile due to G_z, z was scaled with λ⁸:

$$\lambda = \frac{G_{slice}}{G_{slice} + G_z}$$

The integral in Equation (1) was solved by numerical integration with the following assumptions for each slice: linear field Δω(z,z_i)=Δω₀(z_i)+G_z(z_i)*(z-z_i), φ₀(z_i)=const. and TR>>T1. G_z was obtained from the ΔB₀-map.

MRI sequence: An adapted multi-echo gradient echo sequence (mGRE) was developed with two different sinc-Hanning-windowed pulses and variable polarity of G_slice (R₂^*-mapping: Bandwidth-Time-Product BWT=2.7 and pulse duration T_pulse=2ms, MWF-mapping: BWT=2; T_pulse=1ms).

Phantom R₂^*-mapping: A plastic cylinder (Ø=12cm; length=25cm) was filled with 110µmol/l Magnevist® doped agarose gel (5g/l) and scanned with positive and negative G_slice polarity (α=30°/90°; TE1/ΔTE/TR=5ms/5ms/3s; 32 monopolar echoes BW=500Hz/Px; resolution=1x1x4mm³; 25 slices). B₁-map was derived from Bloch-Siegert shift⁹.

In-vivo R₂^*-mapping: Three subjects were scanned with the mGRE sequence with positive and negative G_slice (α=90°; TE1/ΔTE/TR=5ms/5ms/2.5s; 20 monopolar echoes BW=500Hz/Px; resolution=1x1x2mm³; 31 slices) and B₁-mapping.

In-vivo MWF-mapping: One subject was scanned with the mGRE sequence (positive G_slice; α=90°; TE1/ΔTE/TR=2.37ms/2.2ms/2s; 32 bipolar echoes BW=500Hz/Px; resolution=1.1x1.1x4mm³; 25 slices; two averages; scan time 11min).

All measurements were performed on a clinical 3T scanner (Magnetom PRISMA, Siemens).

Analyses: For R₂^*-mapping F(z_i,t) was calculated with and without B₁⁺ and λ-correction. Then Equation (3) was minimized to fit R₂^*. For comparison, R₂^* was estimated from a conventional fit (F(z_i,t)=1). MWF-maps were obtained by fitting once the measured data and once the data divided by F(z_i,t) (regularized) to a multi-exponential model¹⁰. Cut-off for myelin water T₂^*_my < 25ms¹¹.

Results

Phantom: Figure 1 shows R₂^* as function of |G_z| from a conventional fit (F(z_i,t)=1). Compared to α=30°, R₂^* for α=90° is different for +/- G_z and curves are flipped when G_slice polarity is changed. The normalized signal decay (Figure 1) for |G_z|=100µT/m reveals different signal decay for +/- G_z. Incorporating F(z_i,t) resulted in a substantial, up to 5-fold, decrease of R₂^* compared to conventional fitting (Figure 2). Given this strong effect, the difference between using F(z_i,t) with or without including B₁⁺ and λ was smaller, but still visually observable.

In-vivo: Figure 3 shows R₂^*-maps for +/- G_slice as well as their absolute difference maps. While conventional fitted R₂^* show substantial differences, results with F(z_i,t) are less influenced. The difference between the models in Figure 4 illustrates that B₁⁺, λ-correction is most effective in areas with high B₁⁺-deviations and strong G_z (e.g. frontal lobe).

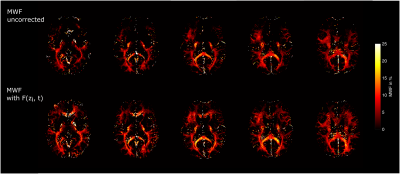
Uncorrected and corrected MWF-maps with F(z_i,t) are illustrated in Figure 5. By using F(z_i,t) it is possible to recover MWF values from the frontal lobe where the conventional fit fails.

Discussion and Conclusion

We have presented a comprehensive numerical model to estimate the dephasing function F(z_i,t) for an arbitrary RF-pulse and slice selection gradient in the presence of G_z. We have demonstrated that the phase along the slice profile is the key factor for modelling F(z_i,t) and that the polarity of the slice selection gradient has to be taken into account. Furthermore, we showed that B₁⁺ variations, especially for high α, and strong G_z affect the slice profile and thus F(z_i,t). Besides R₂^*-mapping, myelin water imaging is an application where our model yields strong improvements in areas affected by G_z (Figure 5).

Acknowledgements

No acknowledgement found.

References

1. Hirsch, N. M. & Preibisch, C. T2* mapping with background gradient correction using different excitation pulse shapes. AJNR. Am. J. Neuroradiol. 34, E65-8 (2013).

2. Hernando, D., Vigen, K. K., Shimakawa, A. & Reeder, S. B. R2*mapping in the presence of macroscopic B0field variations. Magn. Reson. Med. 68, 830–840 (2012).

3. Baudrexel, S. et al. Rapid single-scan T2*-mapping using exponential excitation pulses and image-based correction for linear background gradients. Magn. Reson. Med. 62, 263–268 (2009).

4. Fernndez-Seara, M. A. & Wehrli, F. W. Postprocessing technique to correct for background gradients in image-based R2* measurements. Magn. Reson. Med. 44, 358–366 (2000).

5. Yablonskiy, D. A. Quantitation of intrinsic magnetic susceptibility-related effects in a tissue matrix. Phantom study. Magn. Reson. Med. 39, 417–428 (1998).

6. Preibisch, C., Volz, S., Anti, S. & Deichmann, R. Exponential excitation pulses for improved water content mapping in the presence of background gradients. Magn. Reson. Med. 60, 908–916 (2008).

7. Aigner, C. S., Clason, C., Rund, A. & Stollberger, R. Efficient high-resolution RF pulse design applied to simultaneous multi-slice excitation. J. Magn. Reson. 263, 33–44 (2016).

8. Reichenbach, J. R. et al. Theory and application of static field inhomogeneity effects in gradient-echo imaging. J. Magn. Reson. Imaging 7, 266–279 (1997).

9. Sacolick, L. I., Wiesinger, F., Hancu, I. & Vogel, M. W. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 63, 1315–1322 (2010).

10. Whittall, K. P. & MacKay, A. L. Quantitative interpretation of NMR relaxation data. J. Magn. Reson. 84, 134–152 (1989).

11. Lenz, C., Klarhöfer, M. & Scheffler, K. Feasibility of in vivo myelin water imaging using 3D multigradient-echo pulse sequences. Magn. Reson. Med. 68, 523–528 (2012).

Figures

Figure 1: Comparison between R₂^* from a conventional fit as function of the field gradient G_z for α=30° and α=90 with positive and negative slice selection gradient G_slice. Additionally, the normalized signal decay is plotted for |G_z| = 100µT/m. R₂^* depends on the sign of G_z for α=90° (Note that inverting the G_slice polarity flips R₂^* and magnitude curves), whereas for α=30° R₂^* solely depends on |G_z|.

Figure 2: Phantom data showing the difference between the R₂^*-maps estimated from a conventional fit and maps obtained from the numerical approach for α=30° and α=90° with positive and negative slice selection gradient G_slice. For the numerical approach F(z_i, t) was estimated with and without B₁⁺ and λ-correction. Note that the R₂^* scale for the conventional fit is approx. 5-fold higher than for the corrected models.

Figure 3: Comparison of R₂^*-maps obtained from a conventional fit (upper row), the proposed numerical approach without correction (center row) and with B₁⁺ and λ-correction (bottom row) for positive and negative slice selection gradient G_slice. The absolute difference maps indicate that G_slicepolarity has a substantial effect on R₂^* for the conventional fits and less influence for the numerical models.

Figure 4: Influence of B₁⁺-correction and λ-correction on R₂^*-map estimation. The first two left plots show the difference between the results without and with B₁⁺ and λ-correction for positive and negative slice selection gradient G_slice. The third map shows the corresponding B₁-map and the right one the estimated field gradient map G_z. Differences in the R₂^* maps correlate with B₁⁺ variations and strength of G_z.

Figure 5: Comparison of the MWF obtained by multi-exponential fitting of the GRE magnitude images (top row) and by using the corrected data using F(z_i, t) (bottom row). Note that the proposed model allows to recover MWF values in areas strongly affected by the field gradient G_z (here especially pronounced in frontal areas and fine subcortical fiber bundles).

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

4905