Synopsis

Multi-contrast images of the same anatomy are commonly acquired together to maximize diagnostic information. We demonstrate a multi-channel multi-contrast compressed sensing – parallel imaging (CS-PI) technique that simultaneously uses joint and individual regularization terms to exploit anatomical similarities across contrasts without leakage of distinct features across contrasts and that incorporates coil sensitivities to further improve image quality. The method is compared in-vivo to the single-contrast multi-channel CS-PI method l1-ESPIRiT for PD-/T1-/T2-weighted images of N=11 participants using signal-to-noise ratio calculations as well as neuroradiologist reader studies. The proposed method yields superior performance than l1-ESPIRiT both quantitatively and qualitatively.

Introduction

In many clinical protocols, multi-contrast images of the same anatomy are collected to maximize diagnostic information, resulting in prolonged scan times. Joint compressive sensing (CS) – parallel imaging (PI) reconstructions have been proposed to accelerate these acquisitions ^1-12. When a contrast is reconstructed individually, it is common to use regularization terms such as l1-sparsity and total variation (TV) ^13-15. Yet, when multiple contrasts are reconstructed jointly, group-l1-sparsity ¹⁶ and Color-TV ¹⁷ (CTV) are leveraged to enhance performance ^1-3.

Previous studies have predominantly exclusively considered either individual regularization terms that are suboptimal in joint reconstruction or joint regularization terms that can lead to leakage of distinct features across contrasts. To address these limitations, we recently proposed a joint reconstruction that uses individual and joint terms simultaneously to improve reconstruction quality while preventing leakage of distinct features across contrasts ¹⁸. Here, we introduce a generalized version of the technique that leverages not only multiple-acquisitions but also coil sensitivities to further improve image quality. The multi-channel multi-contrast method, named SIMIT-CS, is compared against a state-of-the-art CS-PI method l1-ESPIRiT ¹⁹.

Methods

The proposed CS-PI reconstruction method solves the following problem:

$$\min_\boldsymbol{x} ~~\alpha_{CTV} CTV(|\boldsymbol{x}|)+\beta_{gL1} ||\boldsymbol{x}||_{2,1}+\gamma_{iTV} \sum_{i=1}^k TV(|\boldsymbol{x}^{(i)} |)+\theta_{iL1} \sum_{i=1}^k||\boldsymbol{x}^{(i)}||_1~~~~~~~~[1]$$

$$\textrm{subject to} ~~||\boldsymbol{A}^{(j,i)}\boldsymbol{x}^{(i)}-\boldsymbol{y}^{(j,i)}||_2\leq \epsilon^{(j,i)},~~~~ i\in 1,...,k~~j\in 1,...,N_c,~~~~~~~~[2]$$

where

$$CTV(|\boldsymbol{x}|)=\sum_n\sqrt{\sum_{i=1}^k [~(\nabla_1|\boldsymbol{x}^{(i)}[n]|)^2 + (\nabla_2|\boldsymbol{x}^{(i)}[n]|)^2~]~}, ~~~~[3] $$

$$||\boldsymbol{x}||_{2,1}=\sum_n\sqrt{\sum_{i=1}^k|\boldsymbol{x}^{(i)}[n]|^2~},$$

$$TV(|\boldsymbol{x}^{(i)}|)=\sum_n\sqrt{(\nabla_1|\boldsymbol{x}^{(i)}[n]|)^2+(\nabla_2|\boldsymbol{x}^{(i)}[n]|)^2~},$$

$$||\boldsymbol{x}^{(i)}||_1=\sum_n|\boldsymbol{x}^{(i)}[n]|,$$

are the regularization terms, $$$\boldsymbol{x}$$$ is a concatenation of all individual contrasts $$$\boldsymbol{x}^{(i)}$$$, $$$k$$$ is number of contrasts, $$$N_c$$$ is number of coils, $$$\alpha_{CTV},\beta_{gL1},\gamma_{iTV},\theta_{iL1}$$$ denote regularization weight parameters and $$$(\epsilon^{(j,i)})^2$$$ (noise energy for contrast $$$i$$$, channel $$$j$$$) is calculated from the acquired data. The imaging matrices $$$\boldsymbol{A}^{(j,i)}$$$ is the undersampled Fourier transform matrix for contrast $$$i$$$ that also includes the coil sensitivity map for channel $$$j$$$.

Eq. [1] imposes joint and individual regularization terms (Eq. [3]) on each contrast. Eq. [2] incorporates parallel imaging by ensuring that for each contrast and channel, the projection of contrast $$$\boldsymbol{x}^{(i)}$$$ onto channel closely represents the acquired data ($$$\boldsymbol{y}^{(j,i)}$$$). Eqs. [1-3] are solved iteratively using an Alternating-Direction Method-of-Multipliers ¹⁸ algorithm. The reconstruction workflow for SIMIT-CS is summarized in Figure 1.

In-vivo multi-contrast images were acquired from N=11 participants using a 3T scanner (Siemens Healthcare, Erlangen, Germany) with a 32-channel receiver-only head coil. Sequence parameters are listed in Figure 1. All reconstructions were performed on Matlab (The Mathworks Inc., Natick, MA, USA). k-Space data were retrospectively undersampled in two phase-encode directions (readout: superior-inferior). All contrasts were jointly reconstructed for SIMIT-CS. Regularization parameters that were optimized on a numerical phantom for channel-by-channel reconstruction ($$$\alpha_{CTV}/\beta_{gL1}/\gamma_{iTV}/\theta_{iL1}=0.11/0.3/0.037/3.0$$$) were used ¹⁸ for SIMIT-CS without further optimization. While this is sub-optimal, fully-sampled data is not available in practice to optimize parameters on a patient-by-patient basis. Furthermore, this facilitated comparison between multi-channel and channel-by-channel reconstruction. l1-ESPIRiT was used as distributed in the BART toolbox, also without patient-specific optimization.

SIMIT-CS was compared to l1-ESPIRiT via neuroradiologist reader studies for 8-fold 2D-undersampling and in terms of peak signal-to-noise-ratio (pSNR) for R=8, R=10, R=12 and R=16. SIMIT-CS was also compared to the channel-by-channel multi-contrast reconstruction that we previously proposed ¹⁸. The results were evaluated by an experienced neuroradiologist (18 years), while methods were randomized and blindly presented. Wilcoxon signed-rank test was performed on the reader scores for anatomy and artefacts. Fully-sampled data, also reconstructed with l1-ESPIRiT, were used as reference for calculating pSNR. Coil sensitivities for SIMIT-CS were estimated using the same approach as in l1-ESPIRiT ¹⁹.

Results and Discussion

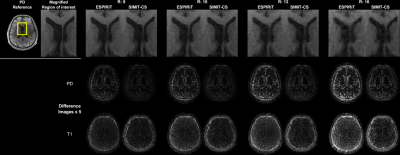
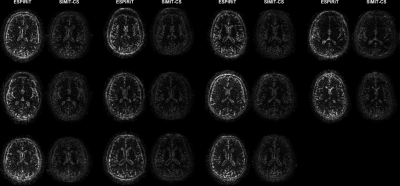
SIMIT-CS reconstructed visually sharper images with less noticeable artefacts consistently across all examined acceleration factors (Figure 2). While both SIMIT-CS and l1-ESPIRiT depict some residual artefacts in lower-SNR T1-weighted images, the intensity of noise-like artefacts is alleviated in SIMIT-CS. Figure 3 clearly demonstrates that SIMIT-CS yields consistently lower artefact levels compared to l1-ESPIRiT across subjects.

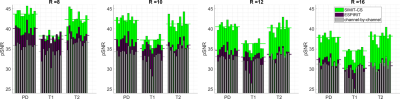
Averaged over contrasts and participants, SIMIT-CS improves pSNR over l1-ESPIRiT by 3.0, 4.2, 5.1 and 5.5dB for R=8,10,12,16, respectively (Figure 4). Note that the benefit of SIMIT-CS reconstruction becomes more apparent towards higher acceleration factors. Meanwhile, compared to a channel-by-channel reconstruction, multi-channel SIMIT-CS improves pSNR by 6.2, 6.4, 6.5, 6.0dB.

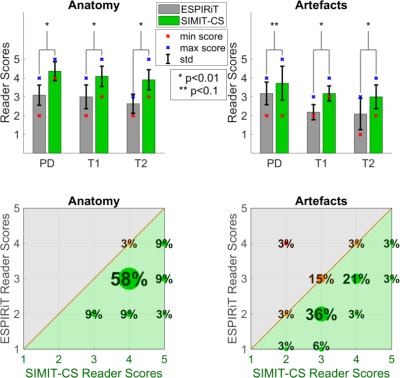
Because the pSNR improvement is lowest at the lowest factor examined, R=8, the methods were further compared via neuroradiologist reader studies at this factor (Figure 5). Overall, SIMIT-CS yields superior performance in 97% of the anatomy scores and 76% of the artefact scores. For all contrasts, SIMIT-CS scores significantly higher in anatomy (p<0.01). It also scores significantly higher in artefact level for all contrasts (p<0.01), except PD-weighted images where the two techniques perform similarly.

Conclusion

Acknowledgements

References

1. Bilgic B, Goyal VK, Adalsteinsson E. Multi-contrast reconstruction with Bayesian compressed sensing. Magn Reson Med 2011;66(6):1601-1615.

2. Majumdar A, Ward RK. Joint reconstruction of multiecho MR images using correlated sparsity. Magn Reson Imaging 2011;29(7):899-906.

3. Huang J, Chen C, Axel L. Fast multi-contrast MRI reconstruction. Magn Reson Imaging 2014;32(10):1344-1352.

4. Majumdar A, Ward RK. Accelerating multi-echo T2 weighted MR imaging: analysis prior group-sparse optimization. J Magn Reson 2011;210(1):90-97.

5. Ilicak E, Senel LK, Biyik E, Cukur T. Profile-encoding reconstruction for multiple-acquisition balanced steady-state free precession imaging. Magn Reson Med 2017;78(4):1316-1329.

6. Knoll F, Holler M, Koesters T, Otazo R, Bredies K, Sodickson DK. Joint MR-PET Reconstruction Using a Multi-Channel Image Regularizer. IEEE Trans Med Imaging 2017;36(1):1-16.

7. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure: k-t SLR. IEEE Transactions on Medical Imaging 2011;30(5):1042-1054.

8. Majumdar A, Ward R. Learning space-time dictionaries for blind compressed sensing dynamic MRI reconstruction. 2015 27-30 Sept. 2015. p 4550-4554.

9. Doneva M, Bornert P, Eggers H, Stehning C, Senegas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med 2010;64(4):1114-1120.

10. Doneva M, Bornert P, Eggers H, Mertins A, Pauly J, Lustig M. Compressed sensing for chemical shift-based water-fat separation. Magn Reson Med 2010;64(6):1749-1759.

11. Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high-resolution diffusion tensor imaging using inter-image correlation. Magn Reson Med 2015;73(5):1775-1785.

12. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 2010;64(3):767-776.

13. Chen SS, Donoho DL, Saunders MA. Atomic Decomposition by Basis Pursuit. SIAM Journal on Scientific Computing 1998;20(1):33-61.

14. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena 1992;60(1):259-268.

15. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58(6):1182-1195.

16. Majumdar A, Ward RK. Compressed sensing of color images. Signal Processing 2010;90(12):3122-3127.

17. Blomgren P, Chan TF. Color TV: total variation methods for restoration of vector-valued images. IEEE Trans Image Process 1998;7(3):304-309.

18. Kopanoglu E, Gungor A, Kilic T, Saritas EU, Cukur T, Guven HE. Joint Reconstruction of Multi-Contrast Images: Compressive Sensing Reconstruction using both Joint and Individual Regularization Functions. 2017; Honolulu, HI, USA. p 3875.

19. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.