4746

Joint Calibrationless Reconstruction of Highly Undersampled Multi-Contrast MR Datasets Using A Novel Low-Rank Completion Approach
Zheyuan Yi1,2,3, Yilong Liu1,2, Yujiao Zhao1,2, Fei Chen3, and Ed X. Wu1,2

1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China, 3Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China

Synopsis

Routine clinical MRI session often requires multi-contrast imaging with identical geometries but different contrasts, and these images of different contrasts are independently reconstructed despite ubiquitous similarities. Simultaneous autocalibrating and k-space estimation (SAKE) provides a powerful calibrationless parallel imaging approach to reduce scanning time through undersampling. However, traditional SAKE reconstruction does not utilize redundant information embedded in multi-contrast datasets. In this study, we propose to advance SAKE by jointly reconstructing concatenated multi-contrast datasets using a novel low-rank completion approach. Our new method explicitly exploits the correlations in multi-contrast datasets and outperforms the traditional SAKE, leading to higher acceleration factors.

Introduction

Routine clinical MRI session often requires multi-contrast imaging with identical geometries but different contrasts. Images of different contrasts are often independently reconstructed despite their ubiquitous similarities. Simultaneous autocalibrating and k-space estimation (SAKE1) is based on low-rank Hankel matrix completion, and it provides a powerful calibrationless parallel imaging approach for scanning time reduction through undersampling. However, traditional SAKE reconstruction does not utilize any redundant information in terms of anatomical structure and coil sensitivity that are uniquely embedded in multi-contrast datasets. Recent studies have attempted to explore the structural similarities among similar datasets by forming low-rank matrices (such as unified tensor regression framework2 and joint-LORAKS3). However, they only dealt with multi-echo or dynamic cardiac datasets where images exhibit extremely rich similarities. We proposed a more generalized framework to jointly reconstruct undersampled multi-contrast datasets based on low-rank matrix completion approach.

Methods

Reconstruction Framework

(1) Construction of Hankel Matrices: For each contrast, multi-channel k-space data are constructed into a Hankel matrix as the same way in SAKE1.

(2) Concatenation of Hankel Matrices: To exploit redundant information, Hankel matrices from different contrast datasets are concatenated side-by-side (Fig. 1a). Such concatenation can be implemented along kernel dimension or along channel dimension of Hankel matrices.

(3) Low-rank Approximation: By enforcing low-rankness on concatenated Hankel matrix along kernel dimension or channel dimension, redundancies in terms of coil sensitivity and anatomical structure are utilized. Utilizations are further inspected (Fig. 2b) using Fourier radial error spectrum plot (ESP, an error metric to quantify the quality of reconstructions as a function of Fourier radius from k-space center4).

(4) Joint Reconstruction: Hankel matrix concatenated along kernel and coil dimensions can both be adopted in joint reconstruction using alternating direction method of multiplier (ADMM5) algorithm (Fig. 1b). Concatenation of Hankel matrix is alternated along kernel dimension and along coil dimension for each iteration. Low-rank constraints increase alternatively, which adopted from incremented-rank power factorization (IRPF6). The whole process is looped with structure and data consistencies until convergence.

Data Acquisition and Retrospective Undersampling

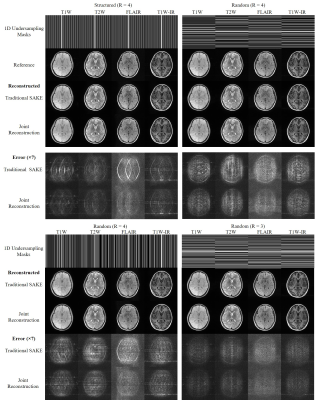
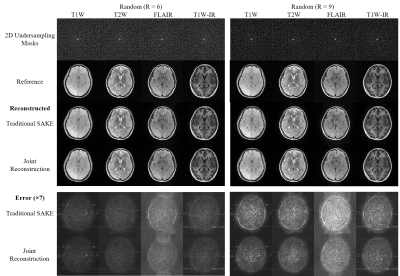
Fully sampled 8-channel multi-contrast datasets (T1W, T2W, FLAIR, and T1W-IR) were acquired on a 3T scanner with identical geometry: FOV = 240×240 mm2 and resolution = 0.8×0.8 mm2. Retrospective 1D undersampling masks with acceleration factors 3 and 4 were randomly generated by discarding lines, and then randomly applied among multi-contrast datasets. Retrospective 2D undersampling masks with acceleration factors 6 and 9 were generated by randomly discarding points.

Results

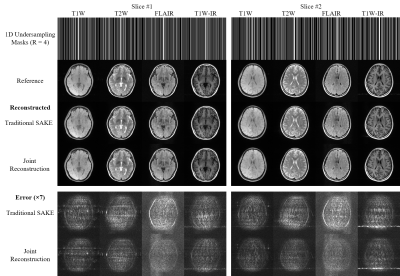
SAKE reconstruction performed on concatenating Hankel matrices along kernel dimension results in generally improved reconstruction in peripheral k-space since it can exploit structural similarity (Fig. 2b). As a complement, concatenating Hankel matrices along coil dimension can provide generally improved reconstruction in central k-space with the utilization of coil sensitivity redundancy. By combining two concatenations, joint reconstruction robustly leads to reduced reconstruction error (Fig. 2a). Similar results are obtained from comparing joint reconstruction to traditional SAKE reconstruction for different slices (Fig. 3); different sampling patterns (Fig. 4); and different acceleration factors (Fig. 4 and Fig. 5). Joint reconstruction is consistently better than traditional SAKE reconstruction of multi-contrast datasets. Improvements become significant at high acceleration factors.

Discussions and Conclusions

Joint reconstruction can exploit both redundancies of coil sensitivity and anatomical structure, leading to reduced reconstruction error compared with traditional SAKE reconstruction. ADMM algorithm adopted in joint reconstruction can robustly mitigate the cross talks stem from dissimilarity among multi-contrast datasets, thus can avoid reaching the local minimum. Joint reconstruction can offer very stable performance and can be applied to high undersampling factor cases when traditional SAKE becomes problematic. For other datasets with such redundant information in terms of coil sensitivity and anatomical structure, our joint reconstruction framework is flexible and can be easily implemented. In this regard, joint reconstruction framework should also be robust in multi-echo datasets and dynamic cardiac datasets.

Acknowledgements

This work was supported by the Hong Kong Research Grant Council (C7048-16G and HKU17103015 to E.X.W.).

References

1. P. J. Shin, et al., "Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion," Magn Reson Med, vol. 72, pp. 959-70, Oct 2014.

2. Joshua D. Trzasko, et. al., "A Unified Tensor Regression Framework for Calibrationless Dynamic, Multi-Channel MRI Reconstruction", ISMRM 2013. No. 603.

3. Bilgic B, et al., "Improving parallel imaging by jointly reconstructing multi‐contrast data." Magn Reson Med, vol. 80.2 pp. 619-632, Aug 2018.

4. Kim, Tae Hyung, and Justin P. Haldar. "The Fourier radial error spectrum plot: A more nuanced quantitative evaluation of image reconstruction quality." In Biomedical Imaging (ISBI 2018), 2018 IEEE 15th International Symposium on, pp. 61-64. IEEE, 2018.

5. Jin KH, et al., ''A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix,'' IEEE 2(4), pp. 480-495. Dec 2016.

6. Haldar, J. P., & Hernando, D. Rank-constrained solutions to linear matrix equations using powerfactorization. IEEE 16(7), pp. 584-587, Jul 2009.

Figures

Figure 1. (a) Framework of joint reconstruction. For each iteration, (1) Hankel matrices are constructed as the way in SAKE; (2) Hankel matrices from different contrast datasets are concatenated side by side; (3) low-rank approximation of Hankel matrix concatenated along kernel or along coil dimension; and (4) structure and data consistency is enforced during joint reconstruction using ADMM. (b) Joint reconstruction with ADMM. For each iteration, concatenation is alternated along kernel dimension and along channel dimension. Low-rank constraints increase alternatively.

Figure 2. (a) Reconstruction error images of 1D 4× undersampling. Multi-contrast datasets are reconstructed using traditional SAKE; SAKE of Hankel matrix concatenated along kernel dimension; SAKE of Hankel matrix concatenated along coil dimension; and joint ADMM algorithm. Reconstruction errors of two concatenations show different characteristics indicated by arrows. Note that joint reconstruction robustly removes artifacts appeared in two concatenation. (b) Fourier radial error spectrum plots of concatenation along kernel and along coil dimension. For all datasets, method of concatenating along kernel dimension results in improved reconstruction in peripheral k-space since it can exploit structure similarity. As a complement, method of concatenating along coil dimension can provide improved reconstruction in central k-space with the utilization of coil sensitivity redundancy.

Figure 3. Reconstruction and error images using traditional SAKE and joint algorithm with 1D 4× undersampling between two slices. Joint reconstruction robustly removes residual aliasing artifacts and is stable between slices.

Figure 4. Reconstruction and error images using traditional SAKE and joint algorithm among different 1D undersampling patterns. Similar results are obtained from different undersampling patterns. Joint reconstruction is consistently better than traditional SAKE.

Figure 5. Reconstruction and error images using traditional SAKE and joint algorithm with 2D undersampling patterns. Joint reconstruction leads to less noise-like artifacts and structural losses than traditional SAKE. Joint reconstruction based on low-rank matrix completion is preferred to implement in 2D undersampling schemes.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
4746