4654
Multi-scale Unrolled Deep Learning Network for Accelerated MRI1Department of Radiology, Stanford University, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 3Department of Electrical Engineering, University at Buffalo, Buffalo, NY, United States, 4Department of Biomedical Engineering, University at Buffalo, Buffalo, NY, United States
Synopsis
Model prior based reconstruction and data-centric prior reconstruction are two strong paradigms in image reconstruction inverse problems. In this abstract, we propose a framework that integrates the model prior and data-centric multi-scale deep learning priors for reconstructing magnetic resonance images (MRI) from undersampled k-space data. The proposed framework brings together the best of both paradigms and has proven superior to conventional accelerated MRI reconstruction techniques.
Purpose
To integrate model prior knowledge into multi-scale deep neural networks for accelerated MRI.Introduction
Deep learning (DL) frameworks have shown tremendous potential in regression and classification problems[1,2]. In DL, we approximate function $$$f(\mathbf{x})$$$ for T training samples $$$ \left\{\mathbf{x}^i,f(\mathbf{x}^i)\right\}_{i\leq T}$$$ over some loss function such that $$$\hat{f}_\theta= \underset{\theta}{\operatorname{argmin}} \mathcal{L}\left(\mathbf{x},f(\mathbf{x}:\theta)\right)$$$, $$$\theta$$$ is DL network parameters. However, such frameworks neglect the model knowledge which is crucial in solving inverse problems where the goal is to find $$$\hat{\mathbf{x}}$$$, given measurements $$$\mathbf{y}$$$ through some data model $$$\mathbf{y}=\phi(\mathbf{x})$$$. In accelerated magnetic resonance imaging (MRI), $$$\phi$$$ is a partial Fourier, $$$\mathbf{y}$$$ is acquired k-space data, and $$$\mathbf{x}$$$ is a desired MR image[3,4]. The system $$$\mathbf{y}=\phi(\mathbf{x})$$$ is under-determined: $$$\mathbf{y}\in\mathcal{C}^M$$$, $$$\mathbf{x}\in\mathcal{C}^N$$$, $$$M<<N$$$. The importance of model knowledge in solving under-determined problems have been investigated in Compressed Sensing (CS) based accelerated MRI frameworks[3,4] by introducing so called data-consistency(model prior) term as shown in (1). Here, we present a framework that integrates the model prior and data-centric multi-scale DL priors: $$\mathbf{x}^*=\arg\min\nolimits_{\mathbf{X}}\underbrace{\left\|\mathbf{y}-\mathbf{\phi}(\mathbf{x})\right\|_{\text{2}}^2}_{\text{model prior}}+\underbrace{\lambda\cal{R}(\mathbf{x})}_{\text{data regularizer}}\quad(1).$$Methods
The schematic model of our framework is shown in Figure.1. It consists of two important constituents:
I) Multi-scale deep learning network : Kernel size and feature maps of convolution filters in deep convolutional neural networks(CNN)[1,2,5] correspond to feature scales. For example, small kernel filters are known to capture high-frequency features such as edges and details whereas bigger kernel filters capture low-frequency features such as structures in images[5,6]. In MRI, low-frequency components (central k-space) capture anatomical structures and higher frequency components capture edges and details. Motivated by this fact and recent development in multi-grid CNN[6] we divide the undersampled MR input image into two different images:- Low-resolution scale (LRS) and high-resolution scale (HRS) images from corresponding lower and higher frequency components in k-space as shown in Figure.1 and 2. A bigger kernel filter with smaller activation map for LRS and vice-versa for HRS image are used and processed through separate DLN pipeline as shown in Figure.1. For its computational advantage, we use convolution based ResNet[7] as shown in Figure.2. Finally, similarly as in [6], multi-scale features from two different DLNs are treated as two channels and combined through a CNN layer.
II) Unrolling DLN : In [8,9] a framework to learn data regularizer from a deep learning based network is proposed such that the regularizer term in (1) is a function of DL network parameter $$$\theta:\cal{R}(\mathbf{x})\rightarrow \cal{R}(\mathbf{x},\theta)$$$. Then to solve (1) with DL prior $$$\cal{R}(\mathbf{x},\theta)$$$, a FISTA[10] based algortihm is used. Specifically, at each $$$i^{th}$$$iteration in deep learning training phase, a proximal gradient based FISTA algorithm with K=4 iterations is solved with current image estimate $$$\mathbf{x}^k$$$ , current deep learning network parameter $$$\theta^{i}$$$ and data model $$$\phi,\mathbf{y}$$$ to obtain new estimate of an image $$$\mathbf{x}^{k+1}$$$ such that, $$$\Gamma\left(\mathbf{x}^k,\phi, \mathbf{y},\mathbf{\theta}^i\right)\rightarrow \mathbf{x}^{k+1}$$$ as shown in Figure.1. For details of unroll network and $$$\Gamma(\cdot)$$$ please refer to [8].
Data and Implementation: Out of 6400 multi-coil knee data slices 60, 20, and 20 percentage were used as the training, validation, and test respectively. A total of 24 undersampling masks with an acceleration factor of 3, 6, 8 were generated using 2 D random undersampling. Conventional data augmentation techniques such as flipping, rotation, and scaling were used for generalization. Complex image values were handled using separate channels for real and imaginary image components. The framework was implemented on Tensorflow 1.10.1. Adam optimizer with $$$\beta_1=0.99,\beta_2=0.99$$$, and learning rate$$$(\alpha)$$$ of 0.0001 to minimize the $$$\ell_1$$$ norm error of the output compared to the ground truth.
Results and Discussions
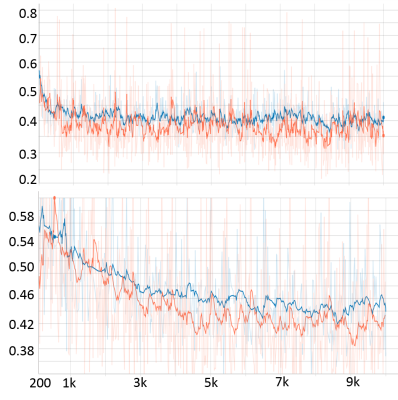
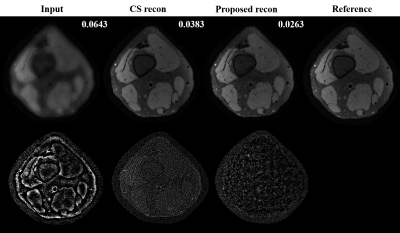
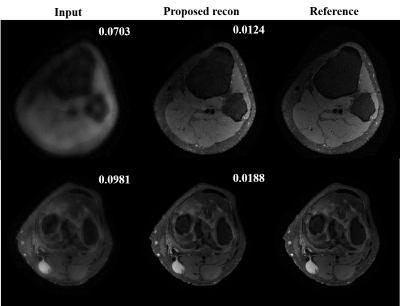
Preliminary results from our proposed framework are presented. Figure.3 shows training and validation loss from the proposed multi-scale network and standard single-scale reconstruction (single resolution: cxc=4x4, F= 128). We can see that the training and validation loss are consistent ensuring there is no overfitting. Improvement in reconstructed image quality compared to the CS based reconstruction[3], and the decrease in the lower bound of loss (~0.32 for the proposed and ~0.38 for the single-scale network are observed as depicted in Figure.4 and Figure.3, respectively. For a fair comparison with data-centric and DL based frameworks[11-14], we are investigating several statistical analysis tools to compare results on the entire test set instead of a comparison between individual images, to be presented in our future presentations. Moreover, we are investigating to answer several key questions in multi-scale DL framework such as, what kind of image features are captured by the lower scale and higher scale deep learning networks and what is an efficient way to combined these features learned from different scales for a better reconstruction.Conclusion
We proposed a novel framework to integrate model prior with multi-scale deep learning network. The proposed framework shows superior results compared to CS and single-scale DL based reconstruction frameworks.Acknowledgements
The work is supported in parts by NIH R01EB009690, NIH R01 EB026136 grants, and GE Healthcare.References
1. A. Krizhevsky, I. Sutskever, and G. Hinton, “Imagenet classification with deep convolutional neural networks”, In NIPS, 2012.
2. Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel, “Backpropagation applied to handwritten zip code recognition”, Neural Computation, 1989.
3. Lustig M, Donoho DL, Pauly JM. “Sparse MRI: The application of compressed sensing for rapid MR imaging”, Magn Reson Med. 2007.
4. D. Liang, E. V. DiBella, R.-R. Chen, and L. Ying, “k-t ISD: Dynamic cardiac MR imaging using compressed sensing with iterative support detection,” Magn Reson Med. 2012.
5. S. Mallat, “ Understanding Deep Convolutional Networks”, arXiv:1601.04920 [stat.ML], 2016.
6. T. Wei Ke, M. Maire, and S. X. Yu, “Multigrid Neural Architecture”. In CVPR, 2016.
7. K. He, X.Zhang, S.Ren, and J.Sun, “Deep Residual Learning for Image Reconstruction”. In CVPR, 2016.
8. S. Diamond, V. Sitzmann, F. Heide, and G. Wetzstein, “Unrolled Optimization with Deep Priors,” arXiv: 1705.08041, 2017.
9. J. Y. Cheng, F. Chen, M. T. Alley, J. M. Pauly, S. S. Vasanawala, “Highly Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering”, arXiv:1805.03300, 2018.
10. I. Daubechies, M. Defrise, and C. De Mol, “An iterative thresholding algorithm for linear inverse problems with a sparsity constraint,” Communications on Pure and Applied Mathematics, 2004.
11. K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock, and F. Knoll, “Learning a Variational Network for Reconstruction of Accelerated MRI Data,” arXiv:1704.00447, 2017.
12. S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, and D. Liang. “Accelerating magnetic resonance imaging via deep learning”. In ISBI, 2016.
13. J. Y. Cheng, F.Chen, M. T. Alley, J. M. Pauly, and S.S. Vasanawala, "Highly Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering", arXiv:1805.03300, 2018.
14. Y. Han, J. C.Ye, "k-Space Deep Learning for Accelerated MRI", arXiv:1805.03779, 2018.
Figures