Synopsis

We introduce a new iterative algorithm for Magnetic Resonance Fingerprinting (MRF) where spatial regularization and fingerprint matching are applied in parallel. This enables to have simultaneously a spatial regularization in addition to the time domain Bloch manifold regularization. Our proposed algorithm showed significant improvements with respect to the state of the art in particular regarding the robustness with respect to measurement noise.

Purpose

Methods:

We introduce a new iterative algorithm for Magnetic Resonance Fingerprinting (MRF) [1] where spatial regularization and fingerprint matching are applied in parallel as in the generalized forward-backward (GFB) algorithm [2]. This enables to have simultaneously spatial regularization in addition to time domain Bloch manifold regularization. The estimated image series X is calculated according to the following three steps described in Figure 1: 1) gradient step to enforce data consistency, 2) in parallel: fingerprint dictionary matching and spatial regularization via total variation (TV) regularization, 3) merging the two parallel branches. After convergence in achieved, a final fingerprint matching is performed to extract the (T1,T2,…) tissue maps. Similar to our previously proposed AIR-MRF [3] and CS-MRF algorithms [4], we exploit on fingerprint SVD compression along the time dimension [5] to accelerate both the matching and the spatial regularization which operates in the compressed domain. The dictionary is compressed to a small rank value (e.g. r=10) to enforce low-rank regularization in a similar way as Zhao et al. [6] and CS-MRF [4]. The three steps iterative algorithm can be formalized as depicted in Figure 1, where $$$\hat{X}_c$$$ is the estimated compressed image series with subscript c indicating the compressed domain, $$$\hat{\theta}$$$ are the estimated T1 and T2 maps, $$$\hat{\rho}$$$ is the estimated proton density map, $$$G=M C^H F S$$$ is the observation operator, which integrates the compression $$$C$$$, the coil sensitivity map $$$S$$$, the Fourier transform $$$F$$$, and the undersampling operator $$$M$$$. $$$\mathcal{R}$$$ is the regularization operator which enforces spatial regularization (TV in our study). The proximal operator is performed via the Chambolle dual algorithm [7] but other implementations such as cycle-spinning provide similar results. We refer to this method as GFB-MRF. Similar initialization and stopping critera as for AIR-MRF are used for GFB-MRF.

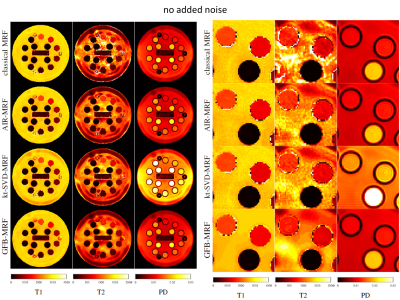
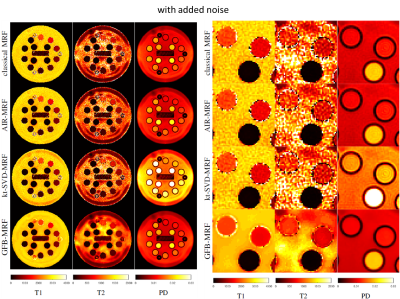
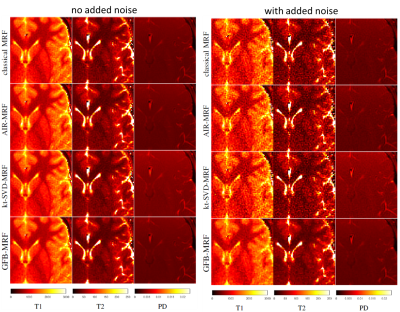
To evaluate the algorithms, the synthetic digital phantom from Brainweb [8] was used with ground truth T1, T2 and proton density maps. In addition, volunteer brain MR data and NIST phantom data were acquired on a MAGNETOM Aera 1.5T MR scanner (Siemens Healthcare, Erlangen, Germany). An unbalanced SSFP sequence prototype was used and data were collected on a single-shot dual-density spiral for each TR. Other acquisition parameter can be found in the AIR-MRF paper [3]. The dictionary contained 5366 atoms with T1 and T2 ranging from 10 to 4500 ms and from 2 to 3000 ms, respectively. The reconstructed parameter maps were compared to the ground truth and errors were quantified using the normalized mean absolute error in percentage. In the case of the Brainweb experiment, we also evaluate the performance of the different methods for different sequence lengths (by cropping the sequence) ranging from 600 to 3000 TRs. In order to validate the robustness of the tested algorithms to realistic conditions, we also performed experiments with added noise in the measurements. In particular, in this case, a Gaussian noise with standard deviation equal to 0.1% of the value of the largest sample of the raw measurement was added to the raw measurements.

GFB-MRF with dictionary compressed at r=10 is compared against the original MRF and other state-of-the-art methods including: AIR-MRF with the dictionary compressed at r=200 components, kt-SVD-MRF [9], and the low-rank method of Zhao et al. [6] with dictionary compressed at r=8 (as suggested by the authors of the method [6]). Experiments were run with prototype implementations in Matlab.

Results:

Discussion and Conclusion

Our proposed iterative GFB-MRF algorithm improved the quality of MRF parameter map estimation and showed improved robustness to noise when compared to the other state-of-the-art methods. The computational load increase compared to AIR-MRF is negligible because spatial regularization is performed in the compressed domain, where only r = 10 components were kept in our experiments.

Disclaimer

Acknowledgements

References

[1] Ma, Gulani, Seiberlich, Liu, Sunshine, Duerk, and Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, Mar. 2013.

[2] H. Raguet, J. Fadili, and G. Peyré, “A generalized forward-backward splitting,” SIAM Journal on Imaging Sciences, vol. 6, no. 3, pp. 1199–1226, 2013

[3] Cline, Chen, Mailhe, Wang, Nadar. AIR-MRF: Accelerated iterative reconstruction for magnetic resonance fingerprinting. Proc. Int. Soc. Magn. Reson. Med., 2016.

[4] S. Arberet, X. Chen, B. Mailhe, P. Speier, and M. S. Nadar, “CSMRF: Sparse & low-rank iterative reconstruction for magnetic resonance fingerprinting,” in ISMRM Workshop on Magnetic Resonance Fingerprinting, 2017

[5] McGivney, D. F., Pierre, E., Ma, D., Jiang, Y., Saybasili, H., Gulani, V., & Griswold, M. A. (2014). SVD compression for magnetic resonance fingerprinting in the time domain. IEEE transactions on medical imaging, 33(12), 2311-2322.

[6] Zhao et al. "Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling." Magnetic Resonance in Medicine (2017).

[7] Chambolle, “An algorithm for total variation minimization and applications,” Journal of Mathematical imaging and vision, vol. 20, no. 1, pp. 89–97, 2004.

[8] “BrainWeb: Simulated Brain Database.” [Online]. Available: http://brainweb.bic.mni.mcgill.ca/. [Accessed: 08-Sep-2015].

[9] Pierre, Griswold, Connelly. Fast Analytical Solution for Extreme Unaliasing of MRF Image Series. Proc. 25th Sci. Meet. Int. Soc. Magn. Reson. Med. 2017