4524
Optimization of MR Fingerprinting Sequence Using a Quantum Inspired Algorithm1Radiology, Case Western Reserve University, School of Medicine, Cleveland, OH, United States, 2Microsoft, Seattle, WA, United States, 3Physics and Astronomy, Texas A&M University, College Station, TX, United States, 4Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 5Case Western Reserve University, School of Medicine, Cleveland, OH, United States
Synopsis
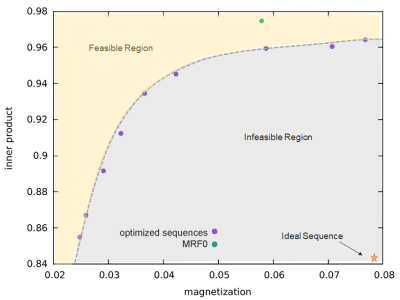
MR Fingerprinting (MRF) is a fast quantitative MR imaging technique that simultaneously quantifies multiple tissue properties. We propose to use quantum-inspired optimization to characterize the optimization landscape by using an appropriate cost function to account for signal features and create an optimization frontier. The simulation results from the optimized MRF sequences showed reduced bias and variance as compared to those from the original empirical design. The in vivo maps from the optimized sequences showed improved image quality as well.
Introduction
MR Fingerprinting1 (MRF) is a fast quantitative MR technique that simultaneously quantifies multiple tissue properties. Given the large number of degrees of freedom in designing the flip angle and TR patterns, optimization of the MRF scan is challenging. Traditional optimization methods are not well-equipped to handle this non-convex and high-dimensional problem, and will likely converge to a local minimum. Here, we propose to use quantum-inspired optimization2 (QIO) to better understand the optimization landscape by using an appropriate cost function to create optimal FA and TR patterns. The QIO methods applied here mimic the effects of quantum mechanics which has been reported to drastically outperform previous classical methods3. They also allow for a flexible cost function that can include any number of additional constraints. Using these algorithms across many different sequence patterns, we have identified an optimization frontier, which appears to define a limits of MRF sequence performance.Method
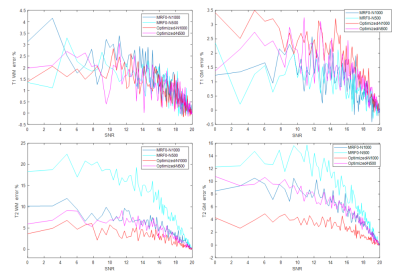
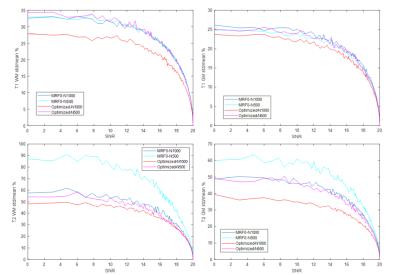
Beginning with an MRF-FISP sequence4, we formulated a cost function to balance four features that are desirable in the MRF signal evolutions, namely, signal magnitude, orthogonality between signals from different tissue types, smoothness, and scan duration. We adapted substochastic Monte Carlo, a quantum-inspired optimization algorithm introduced in [2], to continuous variable problems and applied it to optimize FA and TR patterns to maximize distinguishability between two representative tissue types, white matter (T1 = 800 ms, T2 = 40 ms) and gray matter (T1 = 1400 ms, T2 = 60 ms). Different weights were assigned to each feature in the cost function to generate a frontier representing the trade-off between the inner product of WM and GM and the average signal intensity. The quantitative accuracy, precision and image quality from the optimized and conventional MRF-FISP sequence (MRF0) were evaluated using Monte Carlo simulations and from in vivo scans. For each sequence, signals from GM and WM were simulated with SNR ranging from 0 to 20 dB (10log10(S_signal/S_noise)) with a total of 100 noise levels, where S_signal is the time averaged signal intensity. At each noise level, 2000 repetitions were simulated by adding complex random Gaussian noise. The resulting signal evolutions were matched to the MRF dictionary separately to obtain T1, T2 and M0 values. The mean and standard deviation of the T1 and T2 results at each noise level were calculated and compared to the ground truth. Separately, an in vivo scan was performed in compliance with the IRB and was performed in a Siemens 3T Skyra scanner. Both the optimized and original MRF sequences were applied to the same volunteer with an FOV of 300x300 mm2, image resolution of 1.2x1.2 mm2 using a single shot spiral acquisition, resulting in an acceleration factor of 48.Results
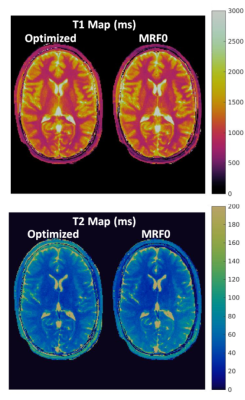
The weights in the cost function were varied to obtain an optimization frontier, which provides an empirical limit for the performance of MRF sequences that are specific to the cost function and constraints used in the optimization. Figure 1 shows one example of the frontier between signal magnitude and orthogonality of the cost function based on gray matter and white matter signals with 1000 TRs, along with the estimate from the conventional empirical design (MRF0). The optimized sequences show better performance on joint magnitude and orthogonality estimation, as demonstrated by a lower inner product between gray and white matter at the same level of average magnetization. Based on the frontiers generated using 1000 TRs and 500 TRs, one sequence optimized for 1000 TR and another optimized for 500 TRs were created by adjusting the weights between signal magnitudes, orthogonality and smoothness. Figure 2 and 3 compare the percentage of mean error and standard deviation of the T1 and T2 results from the optimized and MRF0 sequences from Monte Carlo simulations. At lower SNR, the T1 and T2 results from the optimized sequences have lower bias and variance than those from the MRF0. Figure 4 compares the in vivo T1 and T2 maps from the optimized and MRF0 sequences with single shot spiral acquisition with 1000 TRs. The T2 map from the optimized sequence shows no shading artifacts between frontal and parietal lobes, and thus provides better brain structure contrast in the parietal lobe.Conclusion
Using quantum inspired algorithms, an optimization frontier can be mapped out by accounting for signals’ magnitude, orthogonality and smoothness, which indicate the optimal acquisition parameters of the MRF scans. By taking advantages of this powerful optimization framework, more factors in terms of signal characteristics and actual scan conditions could be incorporated in order to generate the optimal MRF scans under different circumstances.Acknowledgements
The authors would like to acknowledge fundings from Siemens Healthineers, Microsoft and NIH grant NIH 1R01EB016728References
1: Ma et al, "Magnetic Resonance Fingerprinting", Nature, 2013, 495(7440):187-192
2: Jarret, Jordan, and Lackey, "Adiabetic Optimization versus Diffusion Monte Carlo Methods", Physical Review 94(4), 042318
3. Max-SAT 2016 - Eleventh Max-SAT Evaluation. Available at: http://maxsat.ia.udl.cat/results-incomplete/. (Accessed: 5th November 2018)
4. Jiang et al., “MR Fingerprinting Using Fast Imaging with Steady State Precession (FISP) with Spiral Readout.” MRM, 2015,74(6):1621-1631
Figures