4517
Imaging Beyond the Homogeneous Radius in Clinical Magnets1Biomedical Engineering, Yale University, New Haven, CT, United States, 2Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States, 3Department of Neurosurgery, Yale University, New Haven, CT, United States
Synopsis
At the edge of the bore, both B0 and gradient fields have nonlinear distortions which typically make imaging impossible beyond a certain FOV. In this work, we show that undistorted imaging without significant loss of SNR can be achieved outside the typical 50 cm imaging volume using nonlinear spatial encoding techniques. Spatial distortions are corrected by incorporating the nonlinearities of the gradients and B0 field in the encoding equation, while intravoxel dephasing information counteracts spurious intensity modulations and blurring in the reconstructed images.
Introduction
In conventional images encoded with linear gradients, nonlinearities in the main field or the gradients lead to severe signal loss and spatial distortions in reconstructed images. Since a significant fraction of the scanner bore does not meet this criteria, it cannot be used for imaging. For the Siemens 3T Tim Trio scanner, this useful imaging region is a 50 cm sphere, even though the physical width of the bore is 60 cm. Nonlinear gradients have been used for image encoding for over a decade, but those techniques have not previously been applied to reconstructing conventionally acquired images that extend beyond the homogeneous field of view(1). The simulations presented here demonstrate that, using appropriate methods, spatial distortions and SNR losses due to field nonlinearities can be corrected when using the full 60 cm diameter available within the scanner bore.Methods
Simulated signal generation and image reconstruction is performed in Matlab (MathWorks Inc, Natick, Massachusetts, USA).
An object m is encoded according to, $$$S_0=e^{(j Φ(x,t) ) }m$$$, where $$$Φ(x,t)=k^T (t)ψ(x)$$$ and $$$k^T (t)$$$ is the trajectory for a 60 cm FOV, 256x256 Cartesian acquisition of a 3mm transverse slice at isocenter and $$$ψ(x)$$$ are typical gradient and B0 fields provided by Siemens for a 3T MRI scanner (MAGNETOM Trio Tim, Siemens Healthcare, Erlangen, Germany).
In plane and through plane dephasing is incorporated by damping the signal magnitude at each time for a pixel of width $$$W$$$, such that $$$S(t)=S_0 sinc(Wk^T (t) g_x )sinc(Wk^T (t) g_y )sinc(Wk^T (t) g_z )$$$, where $$$g_x=∂ψ/dx$$$, $$$g_y=∂ψ/dy$$$ and $$$g_z=∂ψ/dz$$$. The nonlinear components of the fields are approximated to be linear over one voxel. Mimicking a spin echo acquisition, dephasing is refocused at the center of the acquisition window, and is always incorporated into the signal for all reconstruction methods. Since higher bandwidths can also mitigate the SNR loss and blur caused by dephasing, two bandwidths were considered to illustrate the effect of dephasing: 100 Hz/pix and 1500 Hz/pix.
All reconstructions were performed via conjugate gradient algorithm with 10 iterations using GPU acceleration.
Results
The nonlinearities present in the X and Y gradient fields and the B0 field over the 60 cm FOV, is shown in Fig. 1, subtracting off the pure component of the field. All three of these fields were incorporated into the reconstruction to avoid image distortion and SNR loss.
Using these fields, Figure 2 shows simulations of a low bandwidth acquisition which corresponds to a 10 ms acquisition time. By the end of this readout duration, the phase across a voxel at r=27.5cm (2.5cm outside the standard FOV) is 2pi, which contributes significant intravoxel dephasing. A Fourier transform reconstruction of this data again shows the significant warping, as well as signal loss and blur from dephasing. In this case, a conjugate gradient reconstruction that only incorporates the fields (2nd panel) restores the geometry of the phantom but leaves significant blur. However, a conjugate gradient reconstruction that additionally accounts for intravoxel dephasing, as shown in the 3rd panel, produces an accurate image of the phantom.
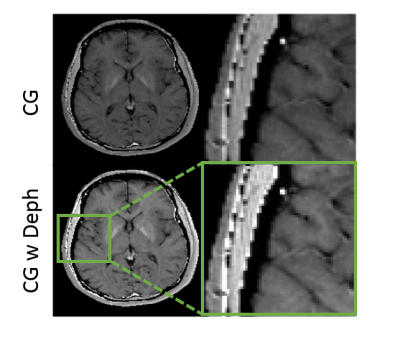
In Fig. 3, the same acquisition and reconstruction are simulated in a numerical brain phantom. Although the spatial distortion is not as apparent in a more clinically relevant phantom, the blur in the first and second panel is removed in panel 3 where intravoxel dephasing is incorporated into the reconstruction.
Fig. 4 shows simulations of a high bandwidth acquisition corresponding to a 0.67 ms acquisition time. In the high bandwidth case, by the end of this readout duration, the phase across a voxel at r=27.5cm is 0.13*pi, which contributes minimal intravoxel dephasing. In this scenario, incorporating a dephasing term may not be necessary. As shown in the second panel, the addition of a dephasing term in the reconstruction provides minimal sharpening of the image.
Discussion
Matrix reconstruction is a flexible means of reconstructing images with arbitrary encoding functions, but accurately representing the signal generation is critical(2). Here we show different scenarios which require accurate knowledge of the field geometry and subvoxel dynamics that can introduce intensity modulations.
In standard Nyquist encoding with linear gradients, there is little winding within a voxel and it is uniform across the FOV, so the resulting intensity modulation is negligible(3). However, when considering nonlinear gradient encoding, the gradient moment that achieves sufficient encoding at the center often creates intravoxel dephasing at the periphery. A similar effect results from nonuniformity in the B0 field, depending on the width of the acquisition window, aka bandwidth. Thus appropriate accounting of intravoxel dephasing becomes important for adequate reconstruction.
Conclusion
It is possible to generate distortion free images without significant blurring or intensity modulation in an extended FOV outside the conventional homogeneous imaging region.Acknowledgements
We would like to acknowledge support from Andrew Dewdney, Stefan Popescu, Edgar Müller, and Peter Dietz at Siemens MR.References
1. Wang H, Tam L, Constable RT, Galiana G.Fast rotary nonlinear spatial acquisition (FRONSAC) imaging. Magn Reson Med 2016; 75(3): 1154-1165.
2. Stockmann J, Ciris P, Galiana G, Tam L, Constable RT. O-Space Imaging: Highly Efficient Parallel Imaging Using Second-Order Nonlinear Fields as Encoding Gradients with No Phase Encoding. Magn Reson Med 2010; 64(2): 447-456
3. Galiana G, Stockmann J, Tam L, Constable RT. Spin Dephasing Under Nonlinear Gradients: Implications for Imaging and Field Mapping. Magn Reson Med 2012; 67: 1120-1126.
Figures