Synopsis

The spatial absolute phase information is important in various stages of MRI scanning, such as parallel image reconstruction, the combination of MR image or MR spectroscopy from each element of multiple receivers and exploration of new contrast and biomarker. Currently, the absolute phase of a transmit field can only be roughly estimated as half of the transceiver phase. This method is not only inaccurate but also not applicable for a transceiver coil. Thus, the accurate estimation of the absolute phase for an arbitrary RF coil system is an unsolved problem and an unmet need of the MR society. Here we propose a new approach to solve this old problem.

INTRODUCTION

The spatial absolute phase information is important in various stages of MRI scanning, such as parallel image reconstruction^{1, 2}, the combination of MR image or MR spectroscopy from each element of multiple receivers³ and exploration of new contrast and bio-marker⁴. Currently, the absolute phase of a transmit field can only be roughly estimated as half of the transceiver phase⁵. This method is not only inaccurate but also not applicable for a transceiver coil. Thus, the accurate estimation of the absolute phase for an arbitrary RF coil system is an unsolved problem and an unmet need of the MR society. Here we propose a new approach to the old problem.

METHODS

RF Phase shimming: Like RF shimming to minimize the non-uniformity of RF field, we can adjust the magnitude and phase of each transmit coil to minimize the absolute phase of a multiple transmit coil. We call this method as RF phase shimming. The transmit coil with RF phase shimming can be used as a reference coil to estimate the B₁⁺ field absolute phase of the multiple transmit coils.

Assumption: The absolute phase of a dual transmit coil system with a quadrature mode is much larger than that with the reference transmit coil.

Theory: A phase of a complex MR image is given:

$ Φ_image = φ_T + φ_B0 + φ_R + φ_s $ (1)

where φ_T is the absolute phase of B₁⁺ of a transmit coil. φ_B0 is the phase accumulation from B₀ inhomogeneity, flow, eddy current, and chemical shift. φ_R is the phase of a receiver coil. φ_s is a synthesized phase which is the sum of reference phases from transmitter radio-frequency synthesizer, receiver radio-frequency synthesizer, and digitizer. According to our hypothesis, the absolute phase Ψ of a targeted transmit coil is given:

$ Ψ = Φ_target + Φ_reference $ (2)

where Φ_target and Φ_reference are the phases of images acquired with target and reference transmit coils, respectively.

Absolute phase of dual transmit coil system: With phantoms and healthy volunteers, we were acquired gradient echo images with different transmit coil modes using identical receive coil configuration and image parameters on a Siemens MAGNETOM Prisma 3.0 T MRI scanner. The Siemens phantom is a 17 cm diameter sphere filled with distilled water, and NiSO4 (1.25 g/liter) x 6 H2O. The phantom images were with the image parameters: FOV 200 x 200 mm², matrix 128 x 128, slice thickness of 1.5 mm, TR/TE = 2000/13 ms, bandwidth = 130 Hz/pixel, and slice number = 2. The scan time for each phantom image is around 4 minutes. The brain images were with the following image parameters: FOV 240 x 240 mm², matrix 128 x 128, slice thickness of 1.5 mm, TR/TE = 3100/13 ms, bandwidth 130 Hz/pixel, and slice number 80. The scan time for each brain image is around 6 minutes.

RESULTS AND DISCUSSION

Figures 1 illustrate the estimation of absolute phase of B₁⁺ of dual transmit coils with a spherical phantom and a quadrature transmit mode. The identical imaging parameters and receive coil generate identical phase shifts caused by B₀ inhomogeneity, absolute phase of a receive coil, and eddy current. According to our hypothesis, the phase image of a reference transmit mode can be approximated to the contribution of other factors excluding to transmit coil. Actually, we can increase the contribution of other factors to image phase by adjusting image parameters, such as increased TE. Thus, the absolute phase of dual transmit coil with the quadrature transmit coil is subtraction of the two phase images acquired by dual transmit coil with the quadrature and reference transmit mode.

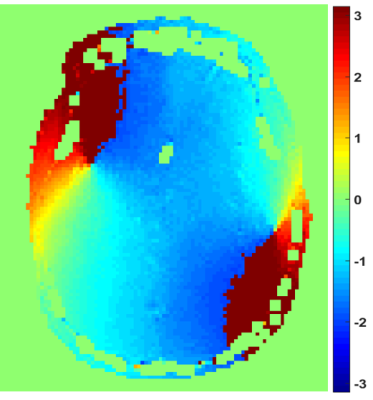
Figures 2 shows the absolute phase of B₁⁺ field in a volunteer’s brain using a dual transmit coils in a quadrature transmit mode. The identical imaging parameters and receive coil generate identical phase shifts caused by B₀ inhomogeneity that resulted from the static magnetic field, susceptibility, flow, chemical shift and eddy current. The subtraction of the two phase images acquired by dual transmit coil with the quadrature and reference transmit mode removes the influence of the B₀ inhomogeneity on the estimation of the absolute phase of B₁⁺ of dual transmit coils with a human brain image. Though our method was validated in the dual transmit coil system, the obtained concept and method will be easy to extend for an arbitrary RF coil system, such as birdcage coil and multi-transmit coil system.

CONCLUSION

In this study, an absolute RF phase of B₁⁺ of dual transmit coil system with a quadrature transmit mode can be determined by the RF phase shimming.

Acknowledgements

References

1. Dagher, J. and K. Nael, MAGPI: A framework for maximum likelihood MR phase imaging using multiple receive coils. Magnetic Resonance in Medicine, 2016. 75(3): p. 1218-1231.

2. Kim, T.H., K. Setsompop, and J.P. Haldar, LORAKS makes better SENSE: Phase‐constrained partial fourier SENSE reconstruction without phase calibration. Magnetic Resonance in Medicine, 2016.

3. Rodgers, C.T. and M.D. Robson, Coil combination for receive array spectroscopy: Are data‐driven methods superior to methods using computed field maps? Magnetic resonance in medicine, 2016. 75(2): p. 473-487.

4. Zhang, X., J. Liu, and B. He, Magnetic-resonance-based electrical properties tomography: a review. IEEE Rev Biomed Eng, 2014. 7: p. 87-96.

5. Katscher, U., et al., Determination of Electric Conductivity and Local SAR via B1 Mapping. IEEE Trans Med Imaging, 2009.