4091

Pseudo-diffusion effects in lung MRI

Lukas Buschle¹, Christian Ziener¹, Thomas Kampf², Volker Sturm³, Ke Zhang¹, Sabine Heiland³, Martin Bendszus³, Heinz-Peter Schlemmer¹, and Felix Kurz³

¹Radiology, German Cancer Research Center, Heidelberg, Germany, ²Neuroradiology, University Hospital Wuerzburg, Wuerzburg, Germany, ³Neuroradiology, University Hospital Heidelberg, Heidelberg, Germany

Synopsis

Magnetic resonance imaging of lung tissue is strongly influenced by susceptibility effects between spin-bearing water molecules and air-filled alveoli. The measured lineshape, however, also depends on the blood-flow around alveoli that can be approximated as pseudo-diffusion. Both effects are quantitatively described by the Bloch-Torrey-equation, which was so far only solved for dephasing on the alveolar surface. In this work, we extend this model to the whole range of physiological relevant air volume fractions. The results agree very well with in vivo measurements in human lung tissue.

Introduction

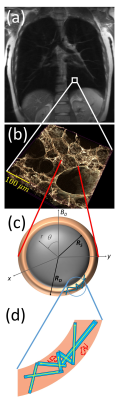
Magnetic resonance imaging of lung tissue is cumbersome due to macroscopic field inhomogeneities, short relaxation times and motion artefacts. While the lineshape of the water peak in most other organs is narrow and Lorenzian-shaped, a broad and asymmetric lineshape is present in lung tissue [1]. On the other hand, an analysis of this broad lineshape reveals microscopic changes of the lung structure [2]. To obtain microstructural parameters from measured lineshapes, it is necessary to understand the signal formation in lung tissue. Previously, a shell model was used to describe the spin dephasing in the magnetic dipole field around alveoli (see [3] and Fig. 1c). However, the signal evolution is not only influenced by the air-filled alveoli but also strongly depends on the blood flow in the highly-vascularized interstitial lung tissue, which can be described as pseudo-diffusion, see Fig. 1d). In this work, both, pseudo-diffusion and susceptibility effects are considered in the so-called extended alveolar surface model that reveals a good agreement with measured lineshapes.

Material and Methods

The susceptibility difference between air-filled alveoli with radius $$$R$$$ and surrounding tissue causes local dipole fields of the form:

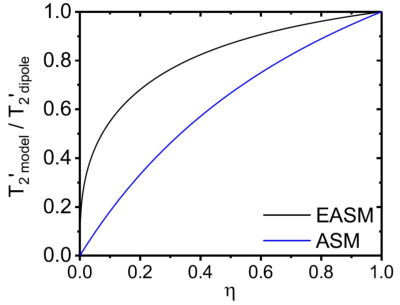
$$\omega(\mathbf{r}) = \delta\omega R^3 \frac{3\cos^2(\theta)-1}{r^3},$$where $$$\delta\omega$$$ denotes the dipole field strength. Pseudo-diffusion and susceptibility effects are described by the Bloch-Torrey-equation that, however, is not analytically solvable for the given form of the magnetic field inhomogeneity. Since the air volume fraction $$$\eta$$$ in lung tissue is typically very high, most spin-bearing particles are located close to the surface of the alveoli, see Fig. 1. Thus, the alveolar surface model assumes that all spins are located on the surface of the alveoli, which allows solving the Bloch-Torrey-equation [4]. For a pathological decrease of the air volume fraction $$$\eta$$$, however, the relaxation time $$$T_2^\prime$$$ is significantly underestimated in this model, see Fig. 2. Therefore, this work extends the alveolar surface model to smaller air volume fractions.

The results are compared with in vivo measurements in a healthy volunteer. Images were acquired with a Magnetom Aera 1.5T (Siemens Healthcare, Erlangen, Germany). A cubic $$$[15\text{mm}]^3$$$ voxel as visualized in Fig. 1a) was selected to acquire the free induction decay in expiration using the PRESS sequence [5] with TR = 1.5 s, echo time TE = 30 ms and twenty averages, see Fig. 1a).

Results

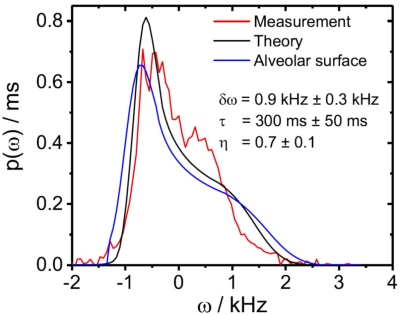
The relaxation time $$$T_2^\prime$$$ in the extended alveolar surface shows a much better agreement with the exact relaxation rate for intermediate air volume fractions $$$\eta$$$ than the previously used alveolar surface model (see Fig. 2). Moreover, the extended alveolar surface model allows an exact solution of the Bloch-Torrey-equation for arbitrary pseudo-diffusion strength. The lineshape strongly depends on the strength of the pseudo-diffusion as shown in Fig. 3: for strong pseudo-diffusion, the lineshape is nearly symmetric and Lorentzian-shaped, whereas the lineshape becomes asymmetric for weaker pseudo-diffusion strength. The results are compared with in vivo measurements in Fig. 4. Obviously, the newly developed extended alveolar surface model agrees better with the experimental data than the alveolar surface model.

Discussion and Conclusion

In this work, the alveolar surface model is extended towards smaller air volume fractions that correspond to pathological changes of the lung microstructure. The extended alveolar surface model allows analyzing susceptibility effects as well as pseudo-diffusion caused by the blood flow in the highly-vascularized interstitial lung tissue. The lineshape highly depends on the pseudo-diffusion strength as shown in Fig. 3. The newly developed model is compared with in vivo measurements is Fig. 4, indicating that the extended alveolar surface model allows a better description of the MR signal evolution than the previously used alveolar surface model. The results are therefore relevant for the analysis of pathological changes, where the air volume fraction is significantly reduced.

Acknowledgements

This work was supported by grants from the Deutsche Forschungsgemeinschaft (Contract Grant number: DFG ZI 1295/2-1 and DFG KU 3555/1-1). L. R.Buschle was supported by Studienstiftung des deutschen Volkes.

References

[1] R.Mulkern, S. Haker, H. Mamata, E. Lee, D. Mitsouras, K. Oshio, M. Balasubramanian, and H. Hatabu. Lung parenchymal signal intensity in MRI: A technical review with educational aspirations regarding reversible versus irreversible transverse relaxation effects in common pulse sequences. Concepts Magn Reson Part A, 43A:29–53, 2014.

[2] J. Zapp, S. Domsch, S. Weingärtner, and L. R. Schad. Gaussian signal relaxation around spin echoes: Implications for precise reversible transverse relaxation quantification of pulmonary tissue at 1.5 and 3 Tesla. Magn Reson Med, 77(5):1938–1945, 2017.

[3] A. G. Cutillo. Application of magnetic resonance to the study of lung. Futura Publishing Company, Inc., Armonk, NY,1996.

[4] L. R. Buschle, F. T. Kurz, T. Kampf, W. L. Wagner, J. Duerr, W. Stiller, P. Konietzke, F. Wünnemann, M. A. Mall, M. O.Wielpütz, H. P. Schlemmer, and C. H. Ziener. Dephasing and diffusion on the alveolar surface. Phys Rev E, 95(2-1):022415, 2017.

[5] P. A. Bottomley. Spatial Localization in NMR Spectroscopy in Vivo. Ann N Y Acad Sci, 508:333–348, 1987.

Figures

Fig. 1: (a) MR imaging of lung tissue highly depends on microscopic field inhomogeneities caused by alveoli (b). A single alveolus is typically described as spherical object (c), where spin-bearing particles are located close to the surface. Blood flow in the highly vascularized tissue, however, also contributes to the signal formation, and can be considered as pseudo-diffusion (d).

Fig. 2: Relaxation times $$$T_2^\prime$$$ for negligible diffusion effects. In the alveolar surface model (ASM), the relaxation rates are significantly underestimated for intermediate air volume fractions $$$\eta$$$ when compared to the exact relaxation rate, whereas the extended alveolar surface model (EASM) is better applicable for small air volume fractions.

Fig. 3: Lineshapes in the extended alveolar surface model for different pseudo-diffusion strength $$$\tau=R^2/D^*$$$. The lineshape is approximately symmetric for strong pseudo-diffusion and becomes more asymmtric with decreasing pseudo-diffusion strength.

Fig. 4: Comparison of the measured lineshape in a healthy subject (red line), the lineshape in the alveolar surface model (blue line) and the lineshape in the newly developed extended alveolar surface model (black line). For realistic values of the peripheral lung tissue, the extended alveolar surface model allows a better description of the flanks of the peak. Please note that no fitted parameters were used.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

4091