3974

Low-Rank Denoising of Magnetic Resonance Elastography Images
Grace McIlvain1, Ariel J Hannum1, Anthony G Christodoulou2, Matthew DJ McGarry3, and Curtis L Johnson1

1Biomedical Engineering, University of Delaware, Newark, DE, United States, 2Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 3Thayer School of Engineering, Dartmouth College, Hanover, NH, United States

Synopsis

Magnetic resonance elastography (MRE) is a phase contrast-based MRI technology that can create whole brain mechanical property maps in vivo. MRE involves the solution of an inverse problem to estimate mechanical properties. Data noise degrades the accuracy of the recovered property images (elastograms). Most MRE acquisitions aim to achieve signal-to-noise ratio (SNR) above a certain threshold, though low SNR is a common issue. We propose a new method to denoise MRE data through spatiotemporal modeling. By approximating MRE data as low-rank, large improvements in SNR can be achieved, which can lead to the ability to salvage MRE data that otherwise would be unusable.

Introduction

Signal noise is a limiting factor in developing higher resolution images in every medical imaging modality, the emerging field of magnetic resonance elastography (MRE) is no exception. MRE is a phase contrast-based MRI technology that can create whole brain mechanical property maps in vivo through mechanical vibration measurements. To accurately calculate MRE mechanical properties through shear wave inversion, a minimum signal-to-noise ratio (OSS-SNR) must be achieved, otherwise property maps can become corrupted. This study aims to filter noise by modeling MRE data as low-rank and exploiting spatiotemporal redundancy in the signal. In this work we demonstrate that the addition of low-rank denoising allows for higher OSS-SNR, potentially salvaging data that would otherwise be un-invertible, while affording no loss in mechanical property calculation accuracy.

Theory

A typical MRE data set can be represented as a single magnitude image modulated by different phase for each encoding direction and time point, which corresponds to a different part of the harmonic vibration cycle. These MRE data sets are fundamentally spatiotemporally redundant1 and can be considered low-rank in the sense that a reduced number of spatial and temporal basis functions can describe the entire dataset2. We can observe the true rank of MRE data by performing singular value decomposition (SVD) on full data sets (Figure 1) and evaluating the root-mean-square error (RMSE) of truncated sets of bases. Figure 1a shows ideal, simulated MRE data and an apparent rank of L=9, compared to the full-rank of 24 (comprising directions, time points, and gradient polarities). It can be assumed that data which resides in higher orders is comprised solely of signal noise (Figure 1b), and removal of this data will lead to data with higher SNR image and potentially improve mechanical property estimation. This is further illustrated through an in vivo brain MRE dataset that shows a similar SVD curve but with potential corruption by non-Gaussian noise at ranks close to L=9 (Figure 1c).

Methods

Low-rank denoising was used post-reconstruction on simulated data with twelve levels (standard deviation) of added Gaussian noise. Simulations were performed using a model of MRE displacements in the human brain[3](2.0 mm resolution; FOV=100x100mm; 20 slices), with simulated k-space, and each was denoised with singular value indices (l) of 15, 12, and 9.Data sets were processed through a nonlinear inversion algorithm[4] (NLI)and through a local direct inversion[5] (LDI) to solve for the complex shear modulus G, which we convert to viscoelastic shear stiffness through μ= 2|G|2/(G’+|G|). RMSE of the wave-motion and the shear stiffness map was found for each data set at each rank. Low-rank denoising was additionally performed on a group 62 in vivo brain MRE datasets acquired as part of a different project. These images had at 2.0x2.0x2.0mm3 resolution and MRE was performed with 50 Hz vibrations. OSS-SNR[6] was measured prior and post low-rank denoising and were filtered using ranks 15, 12, and 9. To identify sources of MRE signal noise, EPI scans were taken in human subjects witheach having25 replicate time points in each data set with 1) motion encoding gradient (MEG) and vibration off, image noise; 2) MEG on and vibration off, physiological noise; and 3) both MEG and vibration on, true MRE data. To analyze this data, we and temporally evaluated differences from median image values at each time point.

Results and Discussion

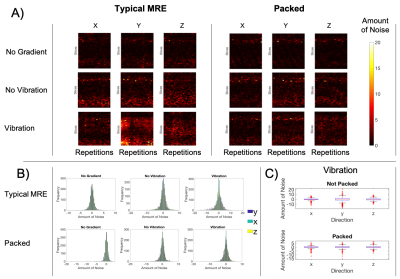
Low-rank denoising considerably improves the OSS-SNR of in vivo MRE data sets (Figure 2), with higher OSS-SNR for ranks 9 and 12. However, the improvement in OSS-SNR varied across subjects, which may represent different original noise characteristics. Through the use of simulations with added noise, it is observed that RMSE of the wave-motion relative to ground truth decreases with lower rank (Figure 3). Interestingly, the two inversion types, NLI and LDI behave slightly differently: LDI accuracy degrades linearly with noise, and shows similar patterns to wave response to denoising, while NLI is consistent to a certain noise threshold, below which noise does not meaningfully impact stiffness calculation, and above which properties are entirely corrupted. Denoising recovers this corrupted data. Remaining noise in vivo not well handled through low-rank denoising is likely a result of imperfect actuation and physiological noise[7]. Vibrational noise primarily occurs in the Y and Z direction and is improved through subject head immobilization (Figure 5). Future work will examine this added noise and potential for denoising.

Conclusion

The ability to understand and denoise MRE images through low-rank methods will allow for the field to move towards higher resolution, faster acquisition scans, making MRE more clinically viable for understanding microstructural brain health.

Acknowledgements

NIH/NIA R01-AG058853, Delaware INBRE (P20-GM103446), and University of Delaware Research Foundation.

References

[1] CL Johnson, JL Holtrop, AG Christodoulou, MDJ McGarry, JB Weaver, KD Paulsen, Z-P Liang, JG Georgiadis, BP Sutton, “Accelerating MR Elastography with Sparse Sampling and Low-Rank Reconstruction,” 22nd Annual Meeting of the International Society for Magnetic Resonance in Medicine, Milan, Italy, May 10-16, 2014, p. 325.

[2] ZP Liang, "Spatiotemporal imaging with partially separable functions." 2007 IEEE Int. Symp. Biomed. Imaging From Nano to Macro, ISBI 2007.

[3] MDJ McGarry, CL Johnson, BP Sutton, JG Georgiadis, EEW Van Houten, AJ Pattison, JB Weaver, KD Paulsen, “Suitability of Poroelastic and Viscoelastic Mechanical Models for High and Low Frequency MR Elastography,” Medical Physics, 2015; 42(2):947-957.

[4] MDJ McGarry, EEW Van Houten, CL Johnson, JG Georgiadis, BP Sutton, JB Weaver, KD Paulsen, “Multiresolution MR Elastography Using Nonlinear Inversion,” Medical Physics, 2012; 39(10):6388-6396.

[5] RJ Okamoto, EH Clayton, PV Bayly, (2011). Viscoelastic properties of soft gels: Comparison of magnetic resonance elastography and dynamic shear testing in the shear wave regime. Physics in medicine and biology. 56. 6379-400.

[6] JP Haldar, ZP Liang, 2010. Spatiotemporal imaging with partially separable functions: A matrix recovery approach. 2010 7th IEEE Int. Symp. Biomed. Imaging From Nano to Macro, ISBI 2010 - Proc. 716–719.

[7] CA Chaze, CL Johnson, “Physiomechanical Noise in Brain Magnetic Resonance Elastography,” 26th Annual Meeting of the International Society for Magnetic Resonance in Medicine, Paris, France, June 16-21, 2018, p. 5596

Figures

Figure 1: Demonstration of low-rank nature of MRE data through singular value decomposition (SVD) of MRE data sets. A) Simulated data with no noise with minimum data rank highlighted; B) simulated data with added Gaussian noise that appears in higher data ranks; and C) in vivo brain data. The gap between in vivo and simulated data may be due to non-Gaussian noise caused by cardiac pulsation or imperfect actuation.

Figure 2: Comparison of OSS-SNR before (full rank) and after low-rank denoising at ranks 15, 12, and 9 in a set of sixty-two in vivo brain MRE datasets. Low-rank denoising improves OSS-SNR, but to varying degrees.

Figure 3: Wave-motion root-mean-square error (RMSE) of simulated images with increasing levels of noise. Images were denoised using truncation to ranks 15, 12, and 9, and improvements in wave-motion with less noise were seen in each case.

Figure 4: Stiffness from nonlinear inversion (NLI) and local direct inversion (LDI) with low-rank denoising. LDI shows increased error with increased noise and is improved at all points through low-rank denoising. NLI shows plateau in which noise does not affect ability to reconstruct values, until a threshold where stiffness properties are unable to be reconstructed, above this threshold low-rank denoising improves image quality. This is illustrated through mechanical property maps inverted from data at different ranks (top row).

Figure 5: Examination of sources of noise in typical a MRE data set. Through 25 repeat temporal measurements, noise in X, Y and Z can be observed slice wise. To reduce head motion during scanning, subject head was packed tightly with small pillows, greatly reducing image noise during vibration.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
3974