3515

Maximising Repeatability: It’s Time to Reconsider the Sampling Scheme for IVIM
Callie Deng1, Pål Erik Goa2, Matthew R. Orton3, Torill E. Sjøbakk1, Tone F. Bathen1, and Neil Peter Jerome1,4

1Department of Circulation and Medical Imaging, Norwegian University of Science and Technology, Trondheim, Norway, 2Department of Physics, Norwegian University of Science and Technology, Trondheim, Norway, 3Division of Radiotherapy & Imaging, Cancer Research UK Cancer Imaging Centre, London, United Kingdom, 4Clinic of Radiology and Nuclear Medicine, St. Olavs University Hospital, Trondheim, Norway

Synopsis

Diffusion-weighted imaging (DWI) has the potential to improve characterisation and detection of breast cancer. A variety of models are available to fit the relationship between MRI signal and b-value, but the repeatability of such models is often overlooked. In this study, we simulate repeated DWI scans and quantify the precision of IVIM parameters from segmented fitting for D and f; our findings suggest that repeatability of f is highly dependent on disproportionate noise at b=0, and repeatability for f and D can be maximised by redistribution of signal averages. Optimal acquisition strategies for varying values of inter-scan noise are reported.

Introduction

Diffusion-weighted imaging (DWI), a technique that infers tissue microstructure via displacement of water molecules, is a staple of oncological imaging. While simple monoexponential fitting of the DWI gives the apparent diffusion coefficient (ADC), a biomarker of cancerous lesions, the intravoxel incoherent motion model (IVIM) attempts to capture underlying tissue microcapillary perfusion through addition of pseudodiffusion parameters.1 It has been demonstrated, however, that high precision measurements of pseudodiffusion parameters are particularly difficult to attain2, thus limiting their transition to clinical use. A minimal approach to IVIM involves segmentation of the DWI signal curve to derive only D and f. While this gives shorter overall scan times, the variability of the resulting parameters is still high.3,4 To better capture and quantify the effects of tissue perfusion, DWI requires acquisition strategies that optimise repeatability of DWI parameters in the context of real, rather than assumed, noise characteristics. In this study, we explicitly characterise the noise in normal liver, an exemplar of highly-perfused tissue, in repeated DWI scans and implement these findings in a simulated dataset for segmented IVIM to derive multiple b-value acquisition sequences that optimise IVIM parameter precision under specified time constraints.

Methods

Noise Estimation in DWI

This prospective study was approved by the regional committee for medical and health research ethics. A single informed, consented volunteer underwent abdominal DWI on a clinical 1.5T scanner (Siemens Healthcare, Erlangen, Germany) with acquisition parameters: coronal orientation, SE-EPI (bipolar encoding), TR/TE: 11600/86ms, FOV: 180x180mm, matrix: 90x90, slice thickness: 2.5mm, slices: 60, iPAT: GRAPPA 2, b-values: 0, 20, 100, 500 s.mm-2. The acquisition was repeated 40 times with all images stored separately for examination of noise characteristics. Identical ROIs containing 2505 voxels were drawn around the whole liver for each signal average image, and the inter-average noise was calculated both on a per voxel basis and for the mean ROI signal at each b-value.

Simulated Data for Optimisation of Segmented IVIM

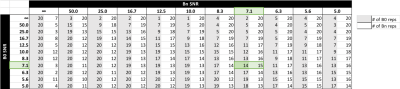
Simulated IVIM data of the normal breast were generated using biexponential parameters specified by While et al5, at b-values 0, 200, 800, with added noise at each b-value reflecting the results obtained from healthy liver. Coefficients of Variation (CoVs) were calculated for IVIM parameters from the repeated simulations over 10,000 voxels. Optimisation of acquisition strategy assumed a scanning session of 3 minutes, with TR 4000 ms per image, and explored total repeatability of IVIM parameters f and D. Repeatability was calculated as a function of independently varying signal averages for b0 and non-zero b-value images. Optimisation was achieved by minimising the function $$$r=abs\left(\frac{\sigma_{D}}{\mu_{D}}\right)+abs\left(\frac{\sigma_{f}}{\mu_{f}}\right)$$$.

Results

Across 40 consecutive scans of a single healthy liver, inter-average noise was normally distributed, with its mean and standard deviation dependent on b-value (Figure 1a). In the ROI containing vasculature, the inter-average noise at b0 was significantly higher at 17.10 compared to a value of 7.70 for b=500. At b0, the SNR was 6.8, compared to an average SNR of 7.0 seen at higher b-values (Figure 1b). The voxel-wise standard deviation of signal intensity reveals that large vascular structures within the liver dominate inter-average noise (Figure 1c), differentially affecting different b-value images as per the profile in Figure 1a, whereas inter-average noise of liver parenchyma is relatively constant across b-values (Figure 1d). This information is critical when designing simulated datasets.

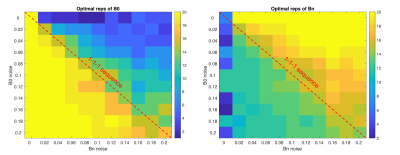
Using this noise profile, the theoretical acquisition strategy that maximised repeatability of segmented IVIM parameters f and D for the simulated breast data in a 3-minute scan was 14 repeats of b0, and 15 repeats of b1 and b2 (Figure 2), deviating substantially from the conventional 1-3-3 arrangement in DWI. Increasing the available scan time also gave similar results, favouring heavily increased sampling of b0 in order to minimise overall variance. Repeating the simulation across a range of inter-scan noise values produced strategies given in Figure 3 and Table 1, showing the dependence of parameter repeatability on noise characteristics at each b-value.

Discussion

DWI modeling is a useful tool with the potential to inform clinical decision making. However, careful evaluation of the repeatability of diffusion-based biomarkers is often neglected. Analysis of the general inter-scan noise characteristics of diffusion parameters, coupled with IVIM simulation, can inform time-efficient DWI acquisition strategies that maximise biomarker repeatability. While traditional DWI acquisition sequences have fewer repeat scans at b=0, our results demonstrate that high inter-scan noise and therefore the need to allocate more scan time at that b-value to maximise IVIM parameter stability.

Acknowledgements

We acknowledge support from the liaison Committee between the Central Norway Regional Health Authority and the Norwegian University of Science and Technology.

References

  1. Koh DM, Collins DJ, Orton MR. Intravoxel incoherent motion in body diffusion weighted MRI: Reality and challenges. AJR Am J Roentgenol. 2011;196:1351–1361. doi: 10.2214/AJR.10.5515.
  2. Jerome NP, Miyazaki K, Collins DJ, et al. (2017) Repeatability of derived parameters from histograms following non-Gaussian diffusion modelling of diffusion-weighted imaging in a paediatric oncological cohort. Eur Radiol 27:345–353.
  3. Meeus EM, Zarinabad N, Manias KA, et al. Diffusion‐weighted MRI and intravoxel incoherent motion model for diagnosis of pediatric solid abdominal tumors. Journal of Magnetic Resonance Imaging. 2018;47(6):1475-1486. doi:10.1002/jmri.25901.
  4. Vidić, I. , Egnell, L. , Jerome, N. P., Teruel, J. R., Sjøbakk, T. E., Østlie, A. , Fjøsne, H. E., Bathen, T. F. and Goa, P. E. (2018), Support vector machine for breast cancer classification using diffusion‐weighted MRI histogram features: Preliminary study. J. Magn. Reson. Imaging, 47: 1205-1216. doi:10.1002/jmri.25873
  5. While, P.T., Teruel, J.R., Vidić, I. et al. Relative enhanced diffusivity: noise sensitivity, protocol optimization, and the relation to intravoxel incoherent motion. Magn Reson Mater Phy (2018) 31: 425. https://doi.org/10.1007/s10334-017-0660-x

Figures

Figure 1: (a) Mean noise across 40 scans as a function of b-value for ROIs with and without large vascular structures. The shaded regions depict the standard deviation of noise. Noise at b0 is significantly higher in ROI containing large vascular structures. (b) SNR as a function of b-value; ROI containing large vascular structures exhibit lower SNR. (c,d) Noise maps corresponding to the standard deviation of signal intensity across 40 scans, per voxel within the liver ROI. Vasculature and surrounding perimeter exhibit greatest noise, which decreases with increasing b-value.

Figure 2: Parameter repeatability in simulated breast tissue, calculated by summing the standard deviation over the mean of f and D, was determined for varying sampling schema. (a) Applying inter-scan noise values derived from liver data to breast IVIM, the theoretical acquisition sequence that maximises parameter repeatability within T=180s is [14, 15, 15] and [10, 10, 10] for T=120s. Time constraints of 120s and 180s are visualised by the dark blue and black step-function contours, respectively. White boxes indicate optimal acquisition strategies. (b, c) Individual contributions of f and D to signal variability.

Table 1: Theoretical acquisition sampling schemes that maximise diffusion parameter repeatability in simulated breast tissue, given a time constraint of T=180s for different SNR. Highlighted in green is the recommended acquisition strategy, [14, 15, 15] based on the noise characteristics quantified in this study. Notice a tendency towards increased sampling at b0 compared to conventional acquisition strategies; as physiological noise increases, indicated by decreasing b0 SNR (down the column), increased sampling should be performed at b0.

Figure 3: Visual representation of Table 1, where noise = 1/SNR. This depicts the optimal distribution of b0 (left) and bn signal averages (right) that maximises diffusion parameter repeatability for varying noise levels, given a time constraint of 180s. The color bar represents the optimal number of repetitions, where warmer colors indicate increased sampling. For b0 noise ≥ bn noise (on or below the dashed red line), more repetitions go toward b0 than bn to maximise parameter repeatability. The conventional 1-3-3 acquisition sequence, or increased sampling of bn, is only optimal when bn noise is significantly greater than b0 noise.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
3515