3343
Acceleration of 3D diffusion MRI using a kernel low rank compressed method1Electrical Engineering, University at Buffalo, State University of New York, buffalo, NY, United States, 2Radiology, New York University School of Medicine, New York City, NY, United States, 3Radiology & Electrical Engineering, Stanford University, Stanford, CA, United States, 4Paul C Lauterbur Research Center for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Shenzhen, China, 5Biomedical Engineering, University at Buffalo,State University of New York, buffalo, NY, United States
Synopsis
Diffusion MRI has showed great potential in probing tissue microstructure and brain structural connectivity. However, high-resolution diffusion MRI with multiple direction is limited by the lengthy scan time. In this abstract, we apply a kernel low rank model to accelerate diffusion imaging by undersampling the k-space. This method is validated using high-resolution mouse brain datasets. Compared with the conventional compressed sensing method, the proposed method demonstrate more accurate mean diffusivity, fractional anisotropy and fiber orientation distribution estimates with acceleration factors up to 8.
Introduction
Diffusion MRI (dMRI)1 has showed great potential in probing tissue microstructure and brain structural connectivity. Among the dMRI techniques, HARDI or DSI is desirable due to its ability to resolve crossing fibers, but requires a large number of diffusion weighted images to be acquired, leading to lengthy acquisition time. Most works accelerate dMRI by undersampling the q-space2-11. Only a few have studied under-sampling the k-space using compressed sensing11-13. In this abstract, we study acceleration of dMRI with under-sampled k-space using a kernel low rank method and demonstrate the superior performance to the conventional compressed sensing in characterize of tissue microstructures.Methods
Reconstruction: In conventional compressed sensing14, know sparsity constraints (in spatial direction) are added to the original linear equation for reconstruction of each DWI, leading to an optimization problem which needs to be solved by nonlinear algorithms. In the KLR method used in this study, a kernel low rank constraint (in diffusion direction) is added to the set of original linear equations for joint reconstruction of all DWIs, where the mathematical representation for the constraint is learned from a number of low resolution images obtained from the fully sampled central k-space data. Kernel principal component analysis, a machine learning approach, is used to obtain the constraint from the training data, which is represented as very few nonlinear diffusion bases. After these diffusion bases are obtained (o.e., the constraint is learned), an optimization problem is solved using an iterative approach enforcing two constraints:(a) each voxel of the reconstructed DWIs along the diffusion direction should be represented by the learned diffusion bases; (b) the k-space data of the reconstructed DWIs should be consistent with acquired data at all locations. The details of the KLR method can be found in [15].
Acquisition&Analysis: KLR method was validated using post-mortem mouse brain (adult C57BL, n=5) data acquired by a horizontal 7T MRI system. The data was acquired using a 3D GRASE sequence described in [16] (TE/TR = 30/600msec, spectral width = 120kHz) with two non-diffusion weighted images and thirty DWIs (b = 2000/mm2, resolution = 0.1 mm isotropic, matrix size = 128x104x180). The fully sampled k-space data was retrospectively under-sampled with reduction factors up to 8 using different 2D variable density under-sampling patterns along ky-kz for different diffusion directions. The reconstructed images were analyzed using Mrtrix3. Mean diffusivity (MD), fractional anisotropy (FA), and fiber orientation distribution (FOD)17 were used as evaluation metrics.
Results
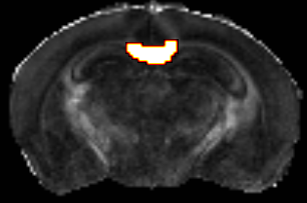
We select several regions of interest, including the corpus callosum (CC)(Fig. 1), cortex, etc, for quantitative evaluation. The proposed method is compared with the conventional compressed sensing method13. Figs. 2-4 shows the percentage errors of the reconstructed mean diffusivity (MD), fractional anisotropy(FA) and fiber orientation distribution (FOD) amplitude, in the CC, with reduction factors of 2-8 using full acquisition as the ground truth. The KLR method showed significantly reduced percentage errors than the conventional compressed sensing method. Specifically, the error of the KLR method is below 5% in MD, 20% in FA and 15% in FOD amplitude for all reduction factors, and below 3% in MD, 10% in FA and 8% in FOD amplitude with reduction factors below 4. Other regions also showed the same trend. Fig. 5 demonstrates that the KLR method preserve the ability to resolve crossing fibers. Here, crossing fibers in the hippocampus estimated from the reduced and full acquisition data remained consistent.Discussion
The superior performance of KLR method is due to the capability to learn and utilize the intrinsic correlation among all DWIs, while the conventional compressed sensing only reconstructs each DWI independently. When the reduction factor is high, the region of fully sampled center k-space needs to be reduced, which affects the accuracy of the correlation information learned from the training data from the fully sampled center k-space. Future work will investigate the effects of motion and SNR to the quantification accuracy for the KLR method. The method will accelerate the acquisition of high-resolution mouse brain dMRI data in basic research and may also be used for future high resolution 3D dMRI of the human brain.Conclusion
In this abstract, we demonstrate the feasibility of accelerating 3D dMRI using the KLR method and the superiority of KLR to the conventional compressed sensing method. Using 3D dMRI data of the mouse brain, we demonstrate that the fiber orientation distribution function and microstructure analyses can be accurately performed at acceleration factors up to 8.Acknowledgements
This work is supported in part by the National Institute of Health R21EB020861, R01EB025133 and R01NS102904.References
[1] KD Merboldt, W Hanicke, J Frahm. Self-diffusion NMR imaging using stimulated echoes. J Magn Reson 1985;64:479-486.
[2] MI Menzel, ET Tan, K Khare, JI Sperl, KF King, XD Tao, CJ Hardy, L Marinelli. Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magn Reson Med. 2011;66:1226-1233.
[3] B Bilgic, K Setsompop, J Cohen-Adad, A Yendiki, L Wald, E Adalsteinsson. Accelerated diffusion spectrum imaging with compressed sensing using adaptive dictionaries. Magn Reson Med. 2012;68:1747-1754.
[4] M Paquette, S Merlet, G Gilbert, R Deriche, M Descoteaux. Comparision of sampling strategies and sparsifying transforms to improve compressed sensing diffusion spectrum imaging. Magn Reson Med. 2014;73:401-416.
[5] O Michailovich, Y Rathi, S Dolui. Spatially regularized compressed sensing for high angular resolution diffusion imaging. IEEE Trans Med Imaging. 2011;30:1100-1115.
[6] A Gramfort, C Poupon, M Descoteaux. Denoising and fast diffusion imaging with physically constrained sparse diction learning. Med Image Anal. 2014;18:36-49.
[7] S Merlet, E Caruyer, A Ghosh, R Deriche. A computational diffusion MRI and parametric dictionary learning framework for modeling the diffusion signal and its features. Med Image Anal. 2013;17:830-843.
[8] S Merlet, R Deriche. Continuous diffusion signal, EAP and ODF estimation via compressive sensing in diffusion MRI. Med Image Anal. 2013;17:556-572.
[9] B Bilgic, I Chatnuntawech, K Setsompop, S Cauley, A Tendiki, L Wald, E Adalsteinsson. Fast dictionary-based reconstruction for diffusion spectrum imaging. IEEE Trans Med Imaging. 2013;32:2022-2033.
[10] A Tobisch, R Stirnberg, RL Harms, T Schultz, A Roebroeck, MMB Breteler, T Stocker. Compressed sensing diffusion spectrum imaging for accelerated diffusion microstructure MRI in long-term population imaging. Front Neurosci. 2018;12:650.
[11] M Pesce, A Repotti, A Auria, A Daducci, JP Thiran, Y Wiaux. Fast fiber orientation estimation in diffusion MRI from kq-space sampling and anatomical priors. IEEE Trans Med Imaging. 2018, [online] Avalilable: http://arxiv.org/abs/1802.02912.
[12] M Mani, M Jacob, A Guidon, V Magnotta, JH Zhong. Acceleration of high angular and spatial resolution diffusion imaging using compressed sensing with multichannel spiral data. Magn Reson Med. 2015;73:126-138.
[13] N Wang, RJ Anderson, A Badea, G Cofer, R Dibb, Y Qi, GA Johnson. Whole mouse brain structural connectiomics using magnetic resonance histology. Brain Struct Funct. 2018;10:1007/s00429-018-1750-x.
[14] M Lustig, D Donoho, JM Pauly. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182-1195.
[15] U Nakarmi, YH Wang, JY Lyu, D Liang, L Ying. A kernel-based low-rank model for low-dimensional manifold recovery in highly accelerated dynamic MRI. IEEE Trans on Med. 2017;36:2297-2307.
[16] D Wu, D Reisinger, J Xu, SA Fatemi, P Zijl, S Mori, JY Zhang. Localized diffusion magnetic resonance micro-imaging of the live mouse brain. NeuroImage. 2014;91:12-20.
[17] JD Tournier, F Calamante, DG Gadian, A Connelly. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage. 2004;23:1176-1185.
Figures