2406

Refined-subspaces for two iteration single shot T2-Shuffling using dictionary matching
Yamin Arefeen1, Nick Arango1, Siddharth Iyer1,2, Borjan Gagoski3,4, Kawin Setsompop2,4,5, Jacob White1, and Elfar Adalsteinsson1,5,6

1Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Fetal Neonatal Neuroimaging and Developmental Science Center, Boston Children's Hospital, Boston, MA, United States, 4Department of Radiology, Harvard Medical School, Boston, MA, United States, 5Harvard-MIT Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Institute for Medical Engineering and Science, Cambridge, MA, United States

Synopsis

Half-Fourier-acquisition-single-shot-turbo-spin-echo (HASTE) serves as a valuable tool for fetal MRI as it is robust to fetal motion and produces images with T2-weighted contrast. However, due to T2-decay and T1-recovery during the acquisition, clinically applied HASTE with sub-180° refocusing pulses and partial-fourier readouts, often yield images with compromised diagnostic quality compared to multi-shot T2-weighted imaging. T2-shuffling exploits a forward model of signal evolution to mitigate blurring and improve contrast in image reconstruction. We propose single-shot imaging with a refined-subspace, iterative application of T2-shuffling, with demonstration in numerical models, that reduces blurring artifacts and improves image contrast in comparison to conventional HASTE.

Introduction

Clinical fetal MRI utilizes 2D-single-shot imaging for T2 contrast, such as Half-Fourier-acquisition-single-shot-turbo-spin-echo (HASTE1, SSFSE), in order to mitigate motion artifacts. However, weighting of k-space due to T2-decay during a lengthy refocusing train results in an image with compromised diagnostic quality.

T2-shuffling2 exploits a forward model of signal evolution to reconstruct multiple, sharp T2-weighted images from a fast-spin-echo acquisition. We propose a two-iteration, refined-subspace T2-shuffling method with dictionary matching3 for single-shot T2-weighted acquisitions to produce images with reduced blurring and improved image contrast in comparison to conventional HASTE, with demonstrations in numerical simulations.

Methods

T2-Shufflng Forward Model:

To fully incorporate signal evolution into the single-shot forward model, one can solve for a time series of images $$$x \in C^{M \times N \times T}$$$. Signal evolutions for HASTE, with realistic T1 and T2 values, when grouped into a dictionary, $$$X$$$, can be well approximated by a low dimensional subspace formed by the dictionary’s left two singular vectors2, $$$\Phi$$$. By projecting $$$x$$$ onto $$$\Phi$$$, one can solve for coefficients, $$$\alpha \in C^{M \times N \times 2}$$$ with the T2-shuffling forward model2,

$$y = R F S \Phi \alpha$$

where $$$R$$$ is the sampling mask, $$$F$$$ is the Fourier transform, and $$$S$$$ are the coil sensitivity operators.

Second Iteration with Refined Basis:

Due to the lengthy echo train and refocusing pulses in HASTE, two singular vectors poorly capture signal evolution from tissue with short T2 values. From an initial shuffling reconstruction, one can utilize dictionary matching3, to compute an approximate T2 estimate for each voxel. Then, one can group voxels based on similar T2 values into $$$B$$$ bins and construct a tighter sub-dictionary, $$$X_i$$$, for each bin and construct a corresponding subspace $$$\Phi_i$$$ for each sub-dictionary. Now each $$$\Phi_i$$$ better represents $$$X_i$$$ since each subspace only needs to represent a smaller range of T2 values. Thus, the total range of T2 values in the total dictionary is much better represented, as illustrated by Figure 1, in both constant flip angle and variable flip angle acquisitions4. On the second iteration of shuffling, the forward model remains unchanged, one just need to apply $$$\Phi_i$$$'s to the appropriate coefficients based on the voxel bin groupings.

Dictionary Matching:

Project $$$\alpha$$$ back into image space, with $$$x = \Phi \alpha$$$. Then, match the computed decay curve at each voxel to a signal evolution in the dictionary, using the l2-norm distance metric. From this match, we estimate a T2 value, which can be used to either group voxels into $$$B$$$ bins or synthesize spin echo contrast.

Numerical Comparison to HASTE:

We obtained T1, T2, proton density, and coil sensitivity maps, from the Brainweb database5. For the following numerical experiments , we used a constant 160° refocusing train and simulated the dictionary with a fixed T1 value of 1 second.

We performed a 2-mm resolution (128 x 128 matrix size) comparison. For single-shot T2 shuffling, we simulated randomly shuffled acquisition of 70 different phase encode lines over time (R= 128/70). For the standard HASTE comparison case, we simulated an R = 2 with 24 auto-calibration lines (ACS) acquisition with conventional linear phase ordering and 5/8, 6/7, and 15/16 partial fourier to achieve desired T2 contrast at central echo times of TE = 75 ms, 125 ms, and 175 ms respectively.

Similarly, we performed a 1-mm resolution comparison (256 x 256 matrix size). Again, we simulated random acquisition of 140 phase encode lines for T2 shuffling (R = 256/140). For the standard HASTE comparison, we maintained the same acceleration, ACS region, and echo times with 9/16, 5/8 , and 6/8 partial fourier.

All acquisitions maintained an echo-spacing of 5 ms, and the second iteration with refined subspaces grouped voxels into 10 different bins. Simulated coil sensitivity profiles and example sampling masks used for reconstruction can be seen in Figure 2.

We solved the T2-shuffling problems with an l1-regularized wavelet prior using BART6,7, HASTE with GRAPPA and projection onto convex sets partial fourier, and the second iteration refined-basis problem with l1-regularized wavelet using fast-iterative-threshold-shrinkage.

Results

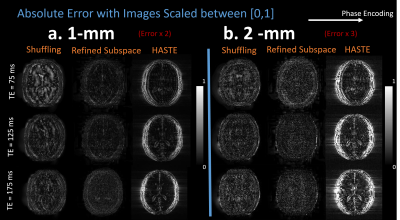
Figures 3 and 4 compare the 2-mm and 1-mm resolution single shot shuffling, refined subspace shuffling, HASTE, and spin-echo images at a variety of echo times, while Figure 5 illustrates the corresponding error maps. Both shuffling reconstructions reduce blurring artifacts in the corresponding HASTE images, while the refined subspace reconstruction more accurately represents spin-echo contrast in comparison to HASTE and single iteration shuffling.

Conclusion

We demonstrated through numerical experiments that T2-shuffling, along with dictionary matching and a second iteration of shuffling with refined subspaces, could be used to improve single-shot T2-weighted image quality.

Acknowledgements

This work was supported in part by NIH research grants R01 EB017337, U01 HD087211, and R01 EB017219. The authors would also like to thank Bo Zhao for providing the numerical phantom.

References

  1. Patel MR, Klufas RA, Alberico RA, Edelman RR. Half-fourier acquisition single-shot turbo spin-echo (HASTE) MR: comparison with fast spin-echo MR in diseases of the brain. AJNR Am J Neuroradiol 1997;18:1635–40.
  2. Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med 2017;77:180–95.
  3. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–92.
  4. Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med 2006;55:1030–7.
  5. Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, et al. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging 1998;17:463–8.
  6. Tamir JI, Ong F, Cheng JY, Uecker M, Lustig M. Generalized Magnetic Resonance Image Reconstruction Using the Berkeley Advanced Reconstruction Toolbox.
  7. Iyer S, Bilgic B, Setsompop K. Faster T2-Shuffling with Wave-Encoding. Presented at the ISMRM Paris, France, June 2018.

Figures

Figure 1: (a) HASTE Refocusing train of 350 ms. (b) Dictionary of signal evolution for a range T2 values between 50 ms - 400 ms. (c) Error in estimating the range of T2 values using a single basis and using refined subspaces and binning. (d) Variable refocusing pulses. (e) Signal evolution for a variety of T2 values. (f) Error in estimating the dictionary using a single basis and using refined subspaces and binning. Note, that one could use variable flip angles to improve specific absorption rate or constant-flip-angles to maintain similarity to HASTE acquisition.

Figure 2: (a) Simulated, 8-channel coil sensitivity maps utilized in the numerical experiments. (b) Randomly shuffled sampling mask used for the 2-mm numerical simulation, with the center phase encode line sampled at 125 ms. (c) Randomly shuffled sampling mask used for the 1-mm numerical simulation, with the center phase encode line sampled at TE=125 ms.

Figure 3: Spin-Echo, Shuffling, Refined Subspace Shuffling, and HASTE reconstructions for a 2 mm acquisition (128 x 128 matrix size) at three echo times. In the shuffling acquisitions, we synthesized spin-echo contrast through estimating T2 values at each voxel with dictionary matching, and picking off the value on the resulting exponential decay curve for each voxel. We simulated acquisition such that we sampled the center phase encode line around the echo times. Both shuffling reconstructions reduces T2 blurring artifacts seen in HASTE. The application of refined subspaces in a second iteration of shuffling also maintains more faithful spin echo contrast.

Figure 4: Spin-Echo, Shuffling, Refined Subspace Shuffling, and HASTE reconstructions for a 1 mm acquisition (256 x 256 matrix size) at three echo times. In the shuffling acquisitions, we synthesized spin-echo contrast through estimating T2 values at each voxel with dictionary matching, and picking off the value on the resulting exponential decay curve for each voxel, based on the echo time. Both shuffling reconstructions reduce T2 blurring artifacts seen in HASTE. Again, notice how the application of refined subspaces maintains more faithful spin echo contrast, in comparison to regular shuffling, particularly in the TE = 75 ms case.

Figure 5: (a) Absolute error maps (x2) in comparison to a spin echo image at three echo times for the 1 mm resolution reconstructions. (b) Absolute error maps (x3) in comparison to a spin echo image at three echo times for the 2 mm resolution reconstructions. Regular shuffling and two iteration basis refined shuffling both reduce image blurring, in comparison to HASTE. However, the refined subspace method maintains more faithful contrast in comparison to the spin echo image. Note, the original images are scaled between [0,1] before computing absolute error maps.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)
2406