2404
Simultaneous multislice reconstruction for spiral MRI using slice-SPIRiT1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States, 2Medicine, University of Virginia, Charlottesville, VA, United States, 3Radiology, University of Virginia, Charlottesville, VA, United States, 4Electrical and Computer Engineering, University of Virginia, Charlottesville, VA, United States
Synopsis
Simultaneous multislice (SMS) imaging provides through-plane acceleration. While current reconstruction methods for non-Cartesian imaging (and also for Cartesian imaging) utilize either in-plane or through-plane coil information, we reasoned that a slice-SPIRiT model could utilize both in-plane and through-plane kernel calibration information, and potentially outperform methods like conjugate-gradient SENSE (CG-SENSE). We developed a slice-SPIRiT method and compared it to CG-SENSE for spiral cardiac cine imaging. Slice leakage artifacts using slice-SPIRiT were 52.9% lower than using CG-SENSE in phantoms, and the artifact power of slice-SPIRiT was 24.2% less than CG-SENSE in five volunteers. Slice-SPIRiT is a promising method for spiral SMS imaging.
Purpose
Simultaneous multislice (SMS) or multiband (MB) imaging provides through-plane acceleration for MRI1, 2. While MB acceleration with CAIPIRINHA3 has signal-to-noise ratio advantages compared to parallel imaging with in-plane undersampling, interslice leakage presents challenges, and this occurs for both Cartesian2 and non-Cartesian methods4. Split slice-GRAPPA2 has been used in Cartesian imaging to reduce slice-leakage and CG-SENSE5 has similarly been used for non-Cartesian imaging. We developed an iterative slice-SPIRiT method to reconstruct spiral SMS images.Theory
We reasoned that a slice-SPIRiT model could utilize both in-plane and through-plane kernel calibration information, and outperform methods like CG-SENSE, which make use of only in-plane coil sensitivity. The proposed slice-SPIRiT reconstruction is illustrated in Figure 1 and the proposed slice-SPIRiT model can be expressed in Equation 1 as follows:
$$\underset{\min}{arg\min}\lVert \left( \sum_{z=1}^{NS}{P_z\cdot D\left ( m_z \right)} \right) -y \rVert ^2 + \lambda _1 \lVert \left (G-I \right) m \rVert ^2+ \lambda _2\lVert m \rVert ^2,$$
where $$${NS}$$$ is the number of MB slices, $$$z$$$ is the slice number,$$$P_z$$$ is the CAIPRINHA phase modulation matrix for the $$$z^{th}$$$ slice, the $$$D$$$ operator performs the Fast Fourier transform $$$(FFT)$$$ and inverse-gridding6 of the Cartesian images, $$$m_z$$$, to the spiral k-space, $$$m_z$$$ is the multicoil image of the $$$z^{th}$$$ slice, $$$y$$$ is the acquired MB spiral data, $$$\lambda _1$$$ is the weight for the in-plane7 calibration consistency, $$$G= \left (\begin{matrix} G_1& \cdots& 0\\\vdots& \ddots& \vdots\\0& \cdots& G_{NS}\\\end{matrix}\right) $$$ is the operator of concatenated in-plane SPIRiT7 kernels, $$$G_z$$$, for the $$$NS$$$ slices, $$$I= \left (\begin{matrix} I_1& \cdots& 0\\\vdots& \ddots& \vdots\\0& \cdots& I_{NS}\\\end{matrix}\right) $$$ is the concatenated unit matrices, $$$m=\left( \begin{array}{c}m_1\\ m_2\\ \vdots\\ m_{NS}\\ \end{array}\right)$$$ is the matrix of concatenated images for the $$$NS$$$ slices, and $$$\lambda _2$$$ is the weight for the Tikhonov regularization in the image domain.
In addition, if we define the operator $$$H=\sum_{z=1}^{NS}{P_z\cdot D}$$$ , then the conjugate of $$$H$$$ is $$$H^*$$$, and $$$H^*$$$ is the key operator to calculate the gradient $$$\nabla _m \left( \lVert H\left( m_z \right) -y \rVert ^2 \right) =2H^*\left( H\left( m_z \right) -y \right)$$$. However, the dimension of the gradient doesn't match the dimension of the concatenated separated slices, $$$m$$$. To solve this problem, we use an approximation for $$$H^*$$$, namely $$$H^*=D_{z}^{*}P_{z}^{*}$$$, where $$$D_{z}^{*}=IFFT\left( SSG_z\cdot C \right)$$$, $$$C$$$ is the gridding operator6, and $$$SSG_z$$$ is the slice-separating kernel as used in the split-slice GRAPPA method2. In this way, the data consistency term in Eq. 1 utilizes the through-plane GRAPPA kernel and enforces joint estimation of the separated slices. LSQR8 is used as the conjugate gradient solver for this model (denoted as CG in Fig.1a).
Methods
SMS spiral gradient-echo cine MRI was performed on a 3T system (Prisma, Siemens) using 30-34 RF channels. For MB RF excitation (MB=3) we employed CAIPIRINHA phase modulation of the multiple slices3. For the reconstruction, we compared the proposed slice-SPIRiT method with CG-SENSE with Tikhonov regularization (weight =0.3). Comparison studies were performed using a phantom and by performing short-axis cine MRI of the heart in five human volunteers. Single-band (SB) images acquired at the same slice locations were used as reference standards. For the phantom and volunteers, SB kernel calibration data using the central 35% of k-space for each slice were acquired in one additional heartbeat appended to the end of the cine acquisition. We used a value of $$$\lambda _1$$$ = 1 based on the SPIRiT model7 and we used $$$\lambda _2$$$ = 1 based on an ad hoc method. The number of iterations for slice-SPIRiT was 3 and for CG-SENSE was greater than 20.Results
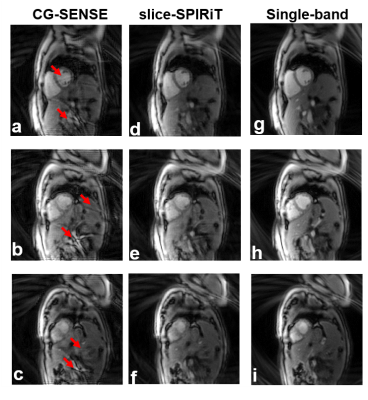
Figure 2 shows a comparison of slice-SPIRiT and CG-SENSE for SMS imaging of a phantom. We found that slice leakage artifacts (assessed using the difference from SB images) of slice-SPIRiT-recovered images (Figure 2j-l) are 52.9% lower than CG-SENSE-recovered images (Figure 2m-o). Results from one of the five human volunteers are shown in Figure 3. The reference SB images at basal, mid-ventricular and apical locations are shown in Figure 3(g-i), and CG-SENSE-recovered MB images 3(a-c) and slice-SPIRiT-recovered MB images (d-f) are shown at the same locations. Red arrows show slice-leakage artifacts in CG-SENSE that are reduced using slice-SPIRiT. Summarizing the results from the 5 volunteers, the artifact power5 of slice-SPIRiT was 24.2% lower than of CG-SENSE (0.138±0.034 vs 0.182±0.037 for slice-SPIRiT vs. CG-SENSE, p<0.05, N=5).Discussion
We developed a slice-SPIRiT reconstruction that uses through-plane calibration consistency, in-plane calibration consistency, and consistency with the acquired MB data. When applied to SMS spiral cardiac cine imaging, the slice-SPIRiT reconstruction performed better than CG-SENSE. Slice-SPIRiT may also be well-suited for variable density spiral data, in-plane undersampling, and SMS Cartesian imaging.Acknowledgements
Acknowledgements: Research support from Siemens Healthineers.References
1. Markus et al. MRM, 2016, 75: 63-81 2. Cauley et al. MRM, 2014, 72: 93 – 102. 3. Breuer et al. MRM, 2005; 53(3): 684-691. 4. Yang et al. MRM, 2018, 00:1-11. 5. Yutzy et al. MRM, 2011; 65(6): 1630-1637. 6. Fessler et al. IEEE T Signal Proces, 2003; 51(2): 560-574. 7. Lustig et al. MRM, 2010, 64: 457 – 471. 8. Paige et al. TOMS, 1982, 8: 43 –71.Figures