2123
PyMRStrain: A Python Library for the Generation of SPAMM, C-SPAMM, and DENSE Synthetic Images1Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, 3Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 4Department of Radiology, School of Medicine, Pontificia Universidad Católica de Chile, Santiago, Chile, 5Institute for Biological and Medical Enginnering, Schools of Engineering, Medicine, and Biological Sciences, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
The generation of synthetic MR images allows the testing of several for postprocessing methodologies under controlled conditions. In this work, we developed an
Introduction
Tagged Magnetic Resonance (TMR) is the most common MR technique for the assessment of the cardiac walls functionality. In this technique, a magnetization grid is generated over the tissue at the beginning of the cardiac cycle, which moves consequently with the cardiac motion. Two of the most popular tagging techniques are Spatial Modulation of Magnetization (SPAMM)1 and Complementary SPAMM (CSPAMM)2, which are based on Stimulated Echoes Acquisition Mode (STEAM). A more recent imaging method is Displacement Encoding with Stimulated Echoes (DENSE)3 which is also based on STEAM sequence and encodes the displacement of the tissue directly in the magnetization phase.
Although there are several validated methods for the postprocessing of SPAMM, C-SPAMM, and DENSE images, new methodologies are rising. For testing purposes, having synthetic images which reproduce the behavior of real MR images would be a very useful tool.
In this work, we developed an efficient open source toolbox for the generation and postprocessing of SPAMM, C-SPAMM and DENSE images, which is based on known expressions of the magnetization and finite element models for the generation of the cardiac geometry and motion.
Methods
Our library uses known SPAMM and DENSE magnetization expressions, obtained from idealized sequence diagrams (see Fig. 1), to generate in-sylico MR images. Thus, the acquired magnetization expressions at time $$$t_n$$$ are:
\[\begin{alignat}{2}M_{\text{SPAMM}}(t_n)&= M\sin(\alpha)\cos^2(\beta) \exp\left(-\frac{t_n}{T_1}\right)+M_0\sin(\alpha)\cos^n(\alpha) \left(1-\exp\left(-\frac{t_n}{T_1}\right)\right)\nonumber\\&-\frac{M}{2}\sin(\alpha)\cos^n(\alpha)\sin^2(\beta)\exp\left(-\frac{t_n}{T_1}\right)\exp\left(-\boldsymbol{i}k_ex\right)\\&-\frac{M}{2}\sin(\alpha)\cos^n(\alpha)\sin^2(\beta) \exp\left(-\frac{t_n}{T_1}\right)\exp\left(+\boldsymbol{i}k_ex\right)\\ \end{alignat}\]
and
\[\begin{alignat}{2}M_{\text{DENSE}}(t_n)&=M_0\sin(\alpha)\cos^n(\alpha)\left\{1-\exp\left(-\frac{t_n}{T_1}\right)\right\} \exp\left\{-\boldsymbol{i}k_e(x+\Delta x)\right\}\\&+\frac{M}{2}\sin(\alpha)\cos^n(\alpha)\exp\left(-\frac{t_n}{T_1}\right)\exp\left(-\boldsymbol{i}k_e\Delta x\right)\\&+\frac{M}{2} \sin(\alpha)\cos^n(\alpha) \exp\left(-\frac{t_n}{T_1}\right)\exp\left\{-\boldsymbol{i}k_e(2x+\Delta x)\right\}\end{alignat}\]
where $$$M_0$$$ represents the thermal equilibrium magnetization, $$$M$$$ the magnetization before the first RF pulse, $$$T_1$$$ the relaxation time, $$$\beta$$$ the flip angle at the times 1 and 3 (see Fig. 1a), $$$\alpha$$$ the flip angle of the acquisition sequence, and $$$x$$$ and $$$\Delta x$$$ the position and the displacement of the tissue, respectively. In the previous expressions, the encoding frequency $$$k_e$$$ controls the motion sensitivity of each imaging modality, and is given by:
$$k_e=\gamma\int_{T_G}G(\tau)~d\tau$$
where $$$\gamma$$$ represents the gyromagnetic constant, and $$$G$$$ and $$$T_G$$$ the strength and duration of the encoding gradient.The generation of images is divided in three main steps: (1) generation of geometry, (2) generation of motion, and (3) magnetization modelling and interpolation. The generation of two dimensional data is based on the work of Glilliam5, in which ranges for geometrical and physiological parameters were defined for simulating "healthy" volunteers and patients. Three-dimensional data can also be generated, but steps (2) and (3) needs to be performed outside of the box. A brief summary of the generation process is given in Fig 2. The core parts of PyMRStrain were written in Python6 and C++, and parallelized using MPI4py7. PyMRStrain runs on Linux, Mac and Windows OS, and can be downloaded from bitbucket.org/hernanmella/pymrstrain. There is also a Matlab-coded part in which self-made implementations of motion estimation techniques such as HARP and SinMod are freely available as well.
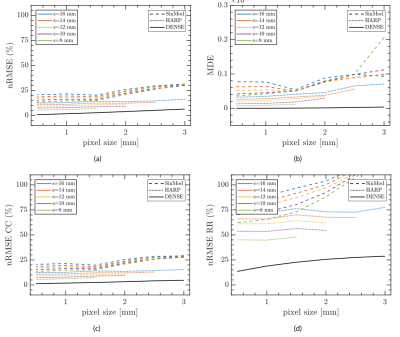
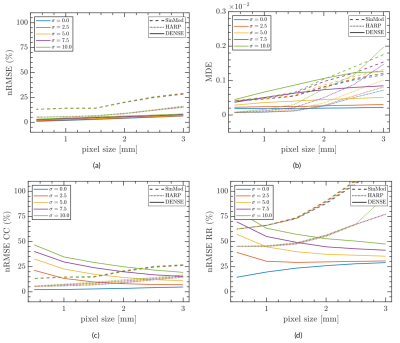
One of the advantages of having synthetical data was tested in this work. Using a dataset of 95 two-dimensional synthetic C-SPAMM and DENSE images, we performed a resolution and noise sensitivity analysis to compare semi-automatic postprocessing tools as HARP, SinMod, and DENSEAnalysis8,9 in the estimation of motion and cardiac strain. Results were compared against exact values, and error was measured using the Normalized Root Square Error (nRMSE) and Directional Error (DE), defined as:
$$nRMSE_a=\sqrt{\frac{\sum_{i=1}^{N}(\lvert a(x)\rvert-\lvert a_e(x)\rvert)^2}{\sum_{i=1}^{N}\lvert a_e(x)\rvert}}$$
$$nRMSE_{\boldsymbol{u}}=\sqrt{\frac{\sum_{i=1}^{N} (\lVert\boldsymbol{u}(x)\rVert_2-\lVert\boldsymbol{u}_e(x)\rVert_2)^2 }{\sum_{i=1}^{N} \lVert\boldsymbol{u}_e(x)\rVert_2}}$$
$$MDE=\frac{1}{N} \sum_{i=1}^{N}\left( 1-\frac{|\boldsymbol{u}(x)\cdot \boldsymbol{u}_e(x)|}{\lVert\boldsymbol{u}(x)\rVert_2\lVert\boldsymbol{u}_e(x)\rVert_2} \right)$$
where $$$N$$$ represents the number pixels in the image and $$$nRMSE_a$$$ (resp. $$$nRMSE_{\boldsymbol{u}}$$$), the $$$nRMSE$$$ for a scalar (resp. vectorial) quantity and subscript $$$()_e$$$ denotes the exact value.
Results
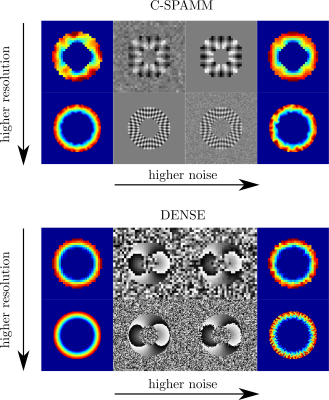
Figures 3 and 4 show the resulting 3D and 2D synthetic images, and the circumferential strain estimated using built-in HARP, SinMod, and DENSEAnalysis. The difference in tag contrasts between SPAMM and C-SPAMM is clearly appreciated in Figs. 3a and 3b, whereas usual wrapping artifacts related to the encoding gradient, can be appreciated in Fig. 3c for DENSE. Regarding the resolution sensitivity analysis, motion and strain are best estimated with DENSE images (Fig. 5), but when noise is added, HARP and SinMod perform better (Fig. 6).Discussion
Synthetic images can reproduce the behavior of SPAMM, C-SPAMM and DENSE images under optimum setups, and non-desired conditions, such as field inhomogeneities and noise presence. The versatility of PyMRStrain is useful to test, under controlled conditions, the sensibility of postprocessing methods under different acquisition and imaging parameters. The code was built in a simplified manner, and new functionalities can be easily added.Conclusion
We developed an open source Python/C++ library for the generation of synthetic SPAMM, C-SPAMM, and DENSE images that is freely available and can be used for testing SPAMM, C-SPAMM, and DENSE images.Acknowledgements
This work has received funding from the projects FONDECYT #1181057 and CONICYT PIA-ACT1416, and the Millenium Science Initiative of the Ministry of Economy, Development, and Tourism, grant Nucleus for Cardiovascular Magnetic Resonance. Mella H. acknowledges the CONICYT scholarship #21170592 for doctoral studies. Sotelo J. thanks to FONDECYT Postdoctorado 2017 #3170737.References
[1] L. Axel and L. Dougherty, “MR imaging of motion with spatial modulation of magnetization.” Radiology, vol.171, no. 3, pp. 841–845, 1989.
[2] S. E. Fischer, G. C. McKinnon, S. E. Maier, and P. Boesiger, “Improved myocardial tagging contrast,” MagneticResonance in Medicine, vol. 30, no. 2, pp. 191–200, aug 1993.
[3] A. H. Aletras, S. Ding, R. S. Balaban, and H. Wen, “DENSE: Displacement Encoding with Stimulated Echoes in Cardiac Functional MRI,” Journal of Magnetic Resonance, vol. 137, no. 1, pp. 247–252, 1999.
[4] J. J. Cao, N. Ngai, L. Duncanson, J. Cheng, K. Gliganic, and Q. Chen, “A comparison of both DENSE and feature tracking techniques with tagging for the cardiovascular magnetic resonance assessment of myocardial strain,” Journal of Cardiovascular Magnetic Resonance, vol. 20, 2018.
[5] A. D. Gilliam and F. H. Epstein, “Automated motion estimation for 2-D cine DENSE MRI,” IEEE Transactions on Medical Imaging, vol. 31, no. 9, pp. 1669–1681, 2012.
[6] G. van Rossum, "Python tutorial", Technical Report CS-R9526, Centrum voor Wiskunde en Informatica (CWI), Amsterdam, May 1995.
[7] L. Dalcin, R. Paz, and M. Storti, MPI for Python, Journal of Parallel and Distributed Computing, 65(9):1108-1115, 2005
[8] B. S. Spottiswoode, X. Zhong, A. T. Hess, C. M. Kramer, E. M. Meintjes, B. M. Mayosi, and F. H. Epstein, “Tracking myocardial motion from cine DENSE images using spatiotemporal phase unwrapping and temporal fitting,” IEEE Transactions on Medical Imaging, vol. 26, no. 1, pp. 15–30, 2007.
[9] A.D.Gilliam and J. D. Suever, “DENSEanalysis” 2016. [Online]. Available: https://github.com/denseanalysis/denseanalysis
[10] Pfaller M., Cruz M., Lang J, Bertoglio C., Wall W., "Parametric model order reduction and its application to inverse analysis of large nonlinear coupled cardiac problems". URL: arxiv.org/abs/1810.12033
Figures