1181
High-Dimensionality Undersampled Patch-Based Reconstruction (HD-PROST) for Accelerated Multi-Contrast Magnetic Resonance Imaging1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
Synopsis
In magnetic resonance imaging, multiple contrasts are exploited to extract clinically relevant tissue parameters and pathological tissue changes. Multi-contrast acquisitions find important applications in parameter mapping (e.g. T1 and T2 mapping) and magnetic resonance fingerprinting. However, these acquisitions lead to long scan times since multiple images with different contrasts need to be acquired. In this study, we present a new reconstruction technique, termed as High-Dimensionality undersampled Patch-based RecOnSTruction (HD-PROST), for highly accelerated 2D and 3D multi-channel multi-contrast MRI.
Purpose
In Magnetic Resonance Imaging (MRI), multiple contrasts are exploited to extract clinically relevant tissue parameters and pathological tissue changes. Multi-contrast acquisitions find important applications in parameter mapping (e.g. T1 and T2 mapping) and magnetic resonance fingerprinting (MRF). However, these acquisitions lead to long scan times since multiple images with different contrasts need to be acquired. In this study, we present a new reconstruction technique, termed as High-Dimensionality undersampled Patch-based RecOnSTruction (HD-PROST), for highly accelerated 2D and 3D multi-channel multi-contrast MRI.Methods
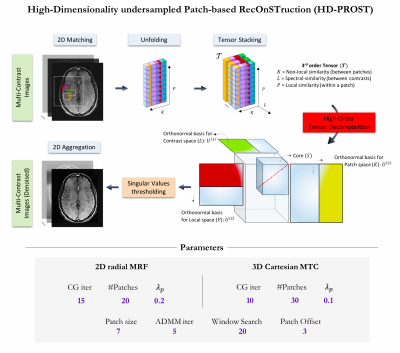
Reconstruction: HD-PROST combines the promising performance of patch-based reconstructions [1,2] and the potential of low-rank image reconstruction through higher-order tensor decomposition [3]. HD-PROST jointly reconstructs multi-contrast 2D or 3D MR images by exploiting the highly redundant information, on a local and non-local scale, and the strong correlation shared between the multiple contrast images (Fig.1). The joint multi-contrast undersampled reconstruction can be combined with parallel imaging and can be formulated as the following joint optimization problem:
$$\mathcal{L}\left(X,\mathcal{T} \right) := \underset{X,\mathcal{T}}{\operatorname{argmin}} \frac{1}{2}\Vert EX-Y \Vert_F^2 + \sum_p \lambda_p \Vert \mathcal{T}_p \Vert_\ast \quad s.t. \quad \mathcal{T}_p = R_p \left( X \right)$$
Where $$$Y$$$ denotes the acquired undersampled data, $$$E$$$ is the encoding operator (including coil sensitivities, Fourier operator, and sampling), and $$$X$$$ denotes the multi-contrast MR images to reconstruct. The operator $$$R_p \left( . \right)$$$ constructs a third order tensor of similar 2D/3D patches from the patch $$$p$$$ centered at pixel $$$p$$$ (see optimization 2). The nuclear norm is used to enforce multi-dimensional low-rank on a multi-contrast patch scale and $$$\lambda_p>0$$$ controls the strength of sparsity. This optimization problem can be solved via alternating direction method of multipliers (ADMM) by iteratively solving the two following sub-problems:
Optimization 1: A regularized multi-contrast MR reconstruction (optimization on $$$X$$$) is performed using the 3D denoised volume ($$$\mathcal{T}$$$) obtained from optimization 2 as prior knowledge. This optimization is solved using the conjugate gradient (CG) algorithm.
Optimization 2: A high-order denoising on a patch level (optimization on $$$\mathcal{T}_p$$$) is performed by building a 3D tensor from similar 2D/3D+L patches (L being the number of contrasts) and applying a high-order singular value thresholding for each block $$$p$$$. The denoised images are then obtained by patch aggregation and used as prior in optimization 1.
2D-MRF Experiments: 2D radial MRF phantom [4] and in vivo brain acquisitions were performed on a 1.5T MR system (Ingenia, Philips) to evaluate the performance of HD-PROST for highly-accelerated simultaneous T1 and T2 mapping. Relevant scan parameters included: radial bSSFP, TE/TR=2/4.4ms, FOV=160x160mm2, resolution=1x1mm2, slice thickness=8mm, bandwidth=723Hz/pixel. One radial spoke was acquired at each time-point (total of 2000 time-points, scan time 8.8seconds) with a flip angle pattern similar to [5]. Five healthy subjects (four men, range 28-37 years) were scanned with the same parameters. The MRF dictionary was generated using the EPG formalism [6] for a T1 in the range of ([50:10:1400,1430:30:1600,1700:100,2200,2400:200:3000]ms) and T2 in the range of ([5:2:80,85:5:150,160:10:300,330:30:600]ms). HD-PROST reconstructions were compared to the low-rank inversion reconstruction (LRI) [7,8].
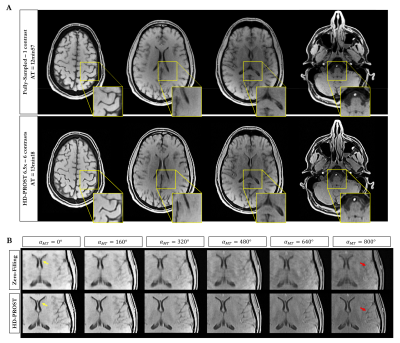
3D-MTC Experiments: In vivo experiments for reconstructing multiple undersampled 3D Magnetization Transfer (MT)-weighted images were conducted on a 1.5T MR scanner (Siemens Magnetom Aera) to illustrate the impact of HD-PROST for high-resolution multi-contrast 3D imaging. Scan parameters included: 3D GRE sequence, axial orientation, FOV=230x230x160mm3, resolution=1x1x2mm3, TE/TR/FA=1.78ms/4.06ms/15°, bandwidth=925Hz/pixel. Six contrasts were acquired with different MT pulse flip angles ($$$\alpha_{MT}=\left[ 0^{\circ}, 160^{\circ}, 320^{\circ}, 480^{\circ}, 640^{\circ}, 800^{\circ} \right]$$$) on two healthy subjects with an accelerated variable density Cartesian sampling with spiral profile order [2,9] (acceleration 6.5x, total scan time for 6 contrasts 13min18s). For comparison purposes, an additional fully-sampled acquisition was performed for the reference image only ($$$\alpha_{MT}=0^{\circ}$$$) (total scan time for a single contrast 12min57s).
Results
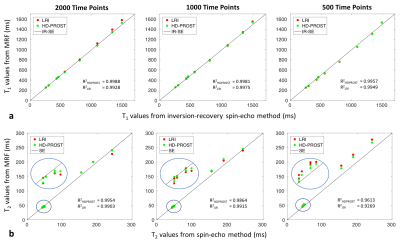
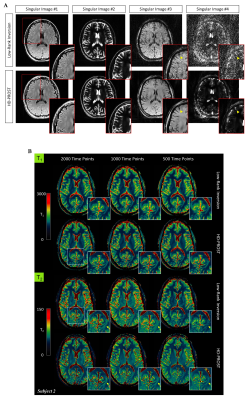
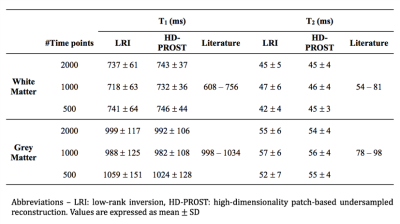
In the 2D MRF phantom study, HD-PROST provides accurate and precise estimation of the T1 and T2 values in comparison to gold standard spin echo acquisitions (Fig.2). HD-PROST achieves good quality (compressed) time-point images (Fig.3a) and quantitative maps (Fig.3b) for the in vivo 2D MRF experiments in comparison to conventional LRI. T1 and T2 values of white matter and grey matter are in good agreement with those reported in the literature for MRF acquisitions (Fig.4) with reduced number of time-point images (500 time-point images, ~2.5sec scan time). For the in vivo MT-weighted 3D acquisitions (6 different contrasts), HD-PROST achieves similar image quality than the fully-sampled reference image for an undersampling of 6.5-fold (Fig.5).Discussion
HD-PROST enables multi-contrast 2D and 3D MR images in a short acquisition time without compromising image quality. Ultimately, this technique may increase the potential of conventional parameter mapping techniques by making efficient use of the rich and redundant information available between the multiple contrast images.Acknowledgements
This work was supported by EPSRC (EP/L015226/1, EP/P001009, EP/P007619, EP/P032311/1) and Welcome EPSRC Centre for Medical Engineering (NS/ A000049/1).References
[1] Akçakaya M, Basha TA, Goddu B, et al. Low-dimensional-structure self-learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magn. Reson. Med. 2011;66:756-767.
[2] Bustin A, Ginami G, Cruz G, et al. Five-minute whole-heart coronary MRA with sub-millimeter isotropic resolution, 100% respiratory scan efficiency, and 3D-PROST reconstruction. Magn. Reson. Med. 2018;00:1-14.
[3] Christodoulou AG, Shaw JL, Nguyen C, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2:215-226.
[4] Captor G, Gatehouse P, Keenan KE, et al. A medical device-grade T1 and ECV phantom for global T1 mapping quality assurance – the T1 mapping and ECV standardization in cardiovascular magnetic resonance (T1MES) program. J. Cardiovascular. Magn. Reson. 2016;18:1-20.
[5] Assländer J, Lattanzi R, Sodickson DK, et al. Relaxation in spherical coordinates: analysis and optimization of pseudo-SSFP based MR-fingerprinting. arXiv:1703.00481.2017:1-22.
[6] Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes – pure and simple. J. Magn. Reson. Imaging 2015;41:266-295.
[7] Zhao B, Lu W, Hitchens TK, et al. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015;74:489-498.
[8] Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn. Reson. Med. 2018;79:933-942.
[9] Prieto C, Doneva M, Usman M, et al. Highly efficient respiratory motion compensated free-breathing coronary mra using golden-step Cartesian acquisition. J. Magn. Reson. Imaging 2014;41(3):738-46.
Figures