1179

Multi-Point 5D Flow MRI - Accelerated Cardiac- and Respiratory-Motion Resolved Mapping of Mean and Turbulent Velocities in 4 Minutes

Jonas Walheim¹, Hannes Dillinger¹, and Sebastian Kozerke¹

¹Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland

Synopsis

This work presents a framework for respiratory motion-resolved multi-point 4D Flow MRI (MP 5D Flow MRI) of mean and turbulent velocities in 4 minutes using a combination of Cartesian Golden angle undersampling, data-driven motion detection and locally low-rank imaging reconstruction. In an imaging study with 9 volunteers, 7-point 5D Flow MRI was compared to a standard, navigator-gated 4-point 4D Flow MRI parallel imaging protocol. Results demonstrate that flow fields from MP 5D Flow MRI in end-expiration agree well with 4D Flow MRI data while scan time was reduced by a factor of 4.5. In addition, MP 5D Flow MRI provides higher accuracy for low velocities and allows assessing TKE over a larger dynamic range compared to 4D Flow MRI.

Introduction

Respiratory-motion resolved 4D flow MRI^1–3 acquires data independently of respiratory motion and exploits similarities among respiratory motion states in the reconstruction. This work presents a framework which combines respiratory-motion resolved reconstruction with multipoint encoding (MP 5D Flow MRI) to provide a robust protocol for the assessment of velocity maps and turbulent kinetic energy⁴ as well as flow conditions in different respiratory motion states.

Methods

Data Acquisition and Reconstruction

Data acquisition and data-driven motion state detection was performed using an undersampled tiny Cartesian Golden angle approach as illustrated in Figure 1⁵. Given the observation that the low-rank property of 4D flow MRI data varies as a function of spatial location⁶, a locally low-rank (LLR)^7,8 approach was used to exploit correlations among heart phases (hp) and respiratory motion states (ms). Data for each velocity encoding were reconstructed separately as

$$\hat{X}_{k_v}=arg \min_x ||\Omega \mathcal{FS}(X_{k_v})-y||_2^2+\lambda\sum_b||R_b(X_{k_v})||_*$$

with undersampling operator $$$\Omega$$$, Fourier transform $$$\mathcal{F}$$$, coil sensitivities $$$\mathcal{S}$$$, k-space data $$$y$$$ and regularization weight $$$\lambda$$$. As illustrated in Figure 2a, the operator $$$R_b$$$ selects patches of size $$$n_x \times n_y \times n_z$$$ in the image from all $$$N_{hp}$$$ heart phases and $$$N_{ms}$$$ motion states and transforms them into a Casorati matrix with dimensions $$$n_x n_y n_z \times N_{hp} N_{ms}$$$.

To ensure accurate quantification of mean and turbulent velocities, a multi-point encoding scheme 9 with 7 different velocity encodings was used 2x3 k_v points + 1 k_v = 0 reference) and a Bayesian approach was employed to combine the data. As illustrated in Figure 2b, velocities and intra-voxel dephasing are determined by maximizing their posterior probability given the measured data⁹.

Imaging Study

Flow in the aortic arch of 9 healthy volunteers was acquired on a 3T Philips Ingenia system (Philips Healthcare, Best, the Netherlands) using the proposed MP 5D Flow MRI and a standard, navigator-gated 4-point 4D Flow MRI approach 10 with a spatial resolution of $$$2.5\times2.5\times2.5mm^3$$$ and 25 cardiac phases. Using the proposed method, velocities were encoded with $$$50cm/s$$$ and $$$150cm/s$$$$ and scan time was fixed to 4 minutes. The 4D reference data (venc: 150cm/s) were acquired using 5mm pencil-beam navigator gating on the diaphragm and, accordingly, the effective scan time depended on the breathing pattern of the subjects. 5D data were sorted into four respiratory motion states. Equation 1 was solved using BART¹¹. LLR reconstructions using only data in end-expiration (EXP) and without gating (NG) were compared to reconstructions exploiting respiratory motion states (5D). Moreover, 5D results obtained with LLR were compared to XD-GRASP⁵. Hyperparameters for LLR and XD-GRASP were automatically tuned for best agreement of velocities in the aorta relative to the 4D reference data.

Data Analysis

Multi-planar reslicing along the aorta was performed using VMTK (www.vmtk.org) and peak flow and peak through-plane velocities were compared using Bland-Altman analysis¹². TKE maps were calculated as in¹³.

Results

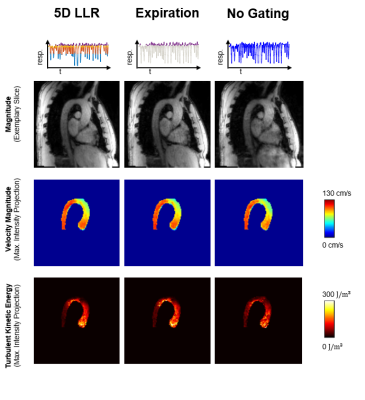
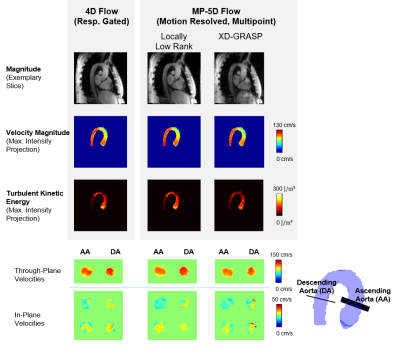
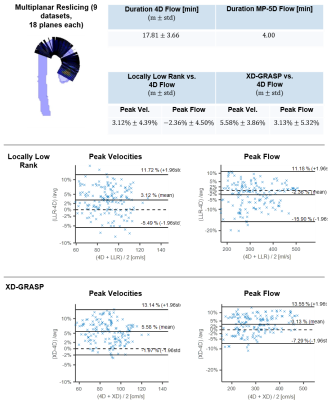
Figure 3 compares reconstruction results of 5D LLR, EXP and NG reconstructions. Magnitude images and TKE maps from 5D LLR reconstructions show less artifacts compared to EXP and NG. Exemplary results of magnitude and velocity magnitude images in expiration obtained with 5D LLR and XD-GRASP are compared relative to the 4D reference results in Figure 4. Maximum intensity projections of velocity magnitudes are similar for all methods whereas TKE maps and magnitude images show more residual aliasing noise for XD-GRASP when compared to 5D LLR. Figure 5 compares results obtained for all 9 volunteers using Bland-Altman analysis. Scan durations for 4D were 17.81+/-3.66min compared to 4 minutes for 5D LLR. On average 5D LLR and XD-GRASP both show good agreement of peak velocities and peak flow relative to the 4D reference.

Discussion

Respiratory-motion resolved reconstruction improves reconstruction accuracy relative to using data from end-expiration only. The acquisition time of MP 5D Flow MRI was 4.5 times shorter on average compared to the 4D Flow MRI reference. Comparing 5D LLR reconstruction with XD-GRASP, both methods showed good agreement of velocity data, however, TKE maps could be more faithfully reconstructed using the 5D LLR approach.

Conclusion

Respiratory motion-resolved multi-point 5D Flow MRI allows for breathing-pattern independent mapping of mean and turbulent velocities in 4 minutes.

Acknowledgements

No acknowledgement found.

References

1. Cheng JY, Zhang T, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Comprehensive Multi-Dimensional MRI for the Simultaneous Assessment of Cardiopulmonary Anatomy and Physiology. Scientific Reports. 2017;7(1):6–9.

2. Jonas Walheim and Sebastian Kozerke. 5D Flow MRI – Respiratory Motion Resolved Accelerated 4D Flow Imaging Using Low-Rank + Sparse Reconstruction. In: Proceedings of the 26th Annual Meeting of ISMRM. Presented at the ISMRM. 2018. p. 0032.

3. Bastkowski R, Weiss K, Maintz D, Giese D. Self-gated golden-angle spiral 4D flow MRI. Magnetic Resonance in Medicine. 2018;80(3):904–913.

4. Dyverfeldt P, Sigfridsson A, Kvitting JE, Ebbers T. Quantification of intravoxel velocity standard deviation and turbulence intensity by generalizing phase-contrast MRI. 2006;(56):850–858.

5. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic resonance in medicine. 2016;75(2):775–788.

6. Giese D, Schaeffter T, Kozerke S. Highly undersampled phase-contrast flow measurements using compartment-based k-t principal component analysis. Magnetic Resonance in Medicine. 2013.

7. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magnetic Resonance in Medicine. 2015;73(2):655–661.

8. Trzasko J, Manduca A, Borisch E. Local versus global low-rank promotion in dynamic MRI series reconstruction. In: Proc. Int. Symp. Magn. Reson. Med. 2011. p. 4371.

9. Binter C, Knobloch V, Manka R, Sigfridsson A, Kozerke S. Bayesian multipoint velocity encoding for concurrent flow and turbulence mapping. Magnetic Resonance in Medicine. 2013;69(5):1337–1345.

10. Dyverfeldt P, Bissell M, Barker AJ, Bolger AF, Carlhäll C-J, Ebbers T, Francios CJ, Frydrychowicz A, Geiger J, Giese D, et al. 4D flow cardiovascular magnetic resonance consensus statement. Journal of Cardiovascular Magnetic Resonance. 2015;17(1):1.

11. Ong F, Uecker M, Tariq U, Hsiao A, Alley MT, Vasanawala SS, Lustig M. Berkeley advanced reconstruction toolbox. Magnetic Resonance in Medicine. 2015;73(2):828–842.

12. Altman DG, Bland JM. Measurement in medicine: the analysis of method comparison studies. The statistician. 1983:307–317.

13. Dyverfeldt P, Sigfridsson A, Kvitting JPE, Ebbers T. Quantification of intravoxel velocity standard deviation and turbulence intensity by generalizing phase-contrast MRI. Magnetic Resonance in Medicine. 2006;56(4):850–858.

14. Cheng JY, Hanneman K, Zhang T, Alley MT, Lai P, Tamir JI, Uecker M, Pauly JM, Lustig M, Vasanawala SS. Comprehensive motion-compensated highly accelerated 4D flow MRI with ferumoxytol enhancement for pediatric congenital heart disease. Journal of Magnetic Resonance Imaging. 2016;43(6):1355–1368.

15. Zhang T, Cheng JY, Chen Y, Nishimura DG, Pauly JM, Vasanawala SS. Robust self-navigated body MRI using dense coil arrays. Magnetic Resonance in Medicine. 2016;76(1):197–205.

Figures

Figure 1: Data acquisition. Data are sampled using a Cartesian pseudo-radial tiny Golden angle sampling pattern¹⁴. Respiratory motion state detection is derived from the k0 profile, which is repeatedly acquired and processed using a combination of principal component analysis, lowpass filtering, and coil-clustering¹⁵. Acquired data are sorted into 4 discrete respiratory motion states such that the acceleration factor for each motion state is similar. The acquisition yields a highly undersampled dataset $$$X \in \mathcal{C}^{N_x \times N_{hp} \times N_{k_v} \times N_{ms}} $$$, with $$$N_x$$$ being the number of samples in the spatial domain, $$$N_{hp}$$$ heart phases, $$$N_{kv}$$$ velocity encodings and $$$N_{ms}$$$ respiratory motion states.

Figure 2: Image reconstruction. a) The locally low-rank model divides the image into 3-dimensional patches. Each patch is reordered into local Casorati matrices for which a low rank is enforced by penalizing the nuclear norm. Compared to a global Casorati matrix, the values of the singular values decrease more rapidly. b) For each Cartesian direction, the different velocity encodings are combined using Bayesian multipoint unfolding. A Bayesian probability model⁹ provides posterior probabilities for mean velocity v and intra-voxel standard deviation σ given the measured signal S. v and σ are chosen such that the posterior probability is maximized, providing maps of TKE and mean velocities.

Figure 3: Comparison of 5D LLR reconstruction with reconstructions from end-expiratory data (EXP) and without gating (NG). 5D LLR data show reduced aliasing noise in the magnitude image. For both EXP and NG, residual motion artifacts are present in the magnitude images and enhanced noise is observed in the TKE maps.

Figure 4: Results in systole and end-expiration comparing MP 5D Flow results reconstructed with LLR and XD-GRASP relative to the 4D reference. For XD-GRASP more residual aliasing noise can be observed in the magnitude images. Moreover, the TKE maps obtained with XD-GRASP show more noise and lower intensities compared to 5D LLR and the 4D reference. Exemplary slices in the ascending aorta (AA) and descending aorta (DA) show qualitatively similar results for through-plane velocities whereas artifacts can be observed in the in-plane velocity components with XD-GRASP.

Figure 5: Comparison of scan times, peak through-plane velocities and peak flow for 5D LLR and XD-GRASP reconstructions compared to the 4D reference in [A1] 9 volunteers. 5D LLR and XD-GRASP show good agreement of peak velocities and peak flow relative to the 4D reference. [A1]Let’s call PI -> 4D reference for clarity.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

1179