Synopsis

Quantitative myocardial perfusion MRI is potentially powerful for diagnosing coronary artery disease. However, It is challenging to accurately measure dynamic contrast enhancement throughout the whole moving heart. Most perfusion methods employ some combination of ECG-triggering, breath-holds, dual-bolus acquisition, and multislice 2D acquisition, leading to difficult workflows and limited spatial coverage. Here we describe a non-ECG, free-breathing, single-bolus, 3D alternative which employs the MR Multitasking framework to perform low-rank tensor imaging. We add 3D respiratory motion compensation to this framework to eliminate the need for breath-holds. This new method is demonstrated and evaluated in healthy volunteers.

Introduction

Quantitative first-pass myocardial perfusion MRI shows great potential for diagnosing coronary artery disease. However, it is challenging to accurately measure fast-changing gadolinium (Gd) concentrations throughout the whole moving heart within a scan time of only 30–60s. These challenges are typically addressed through some combination of ECG-triggering, breath-holds, dual-bolus acquisition, and multislice 2D acquisition, which leads to difficult workflows and limited spatial coverage.

Here we propose a non-ECG, free-breathing, single-bolus, 3D alternative to overcome these limitations. This method employs the MR Multitasking framework¹, which models multidimensional images as low-rank tensors² and which has previously been demonstrated for non-ECG, single-bolus 2D myocardial perfusion. We extend its capabilities to 3D free-breathing perfusion imaging via stack-of-stars encoding and 3D respiratory motion compensation, which has been shown to benefit low-rank perfusion imaging³. This new method is demonstrated and evaluated in healthy volunteers.

Methods

Image Model

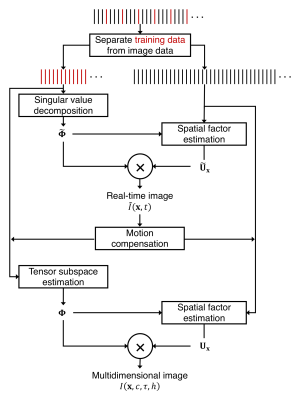
We perform non-ECG time-resolved T1 mapping by obtaining a 6D image $$$I(\mathbf{x},c,\tau,h)$$$ with spatial location $$$\mathbf{x}$$$, cardiac phase $$$c$$$, saturation recovery (SR) time $$$\tau$$$, and heartbeat index $$$h$$$. Respiratory motion is incorporated into the forward model as $$$M_h\{I(\mathbf{x},c,\tau,h)\}$$$, where the spatial transform $$$M_h\{\cdot\}$$$ mimics the effect of respiratory motion at heartbeat $$$h$$$. To accelerate acquisition, we model $$$I$$$ as a low-rank 4-way tensor $$$\mathcal{A}$$$ with elements $$$A_{ijk\ell}=I(\mathbf{x}_i,c_j,\tau_k,h_\ell)$$$. This tensor can be decomposed in collapsed form as$$\mathbf{A}_{(1)}=\mathbf{U_x\Phi},$$$$\mathbf{\Phi=C}_{(1)}(\mathbf{U}_\mathrm{h}\otimes\mathbf{U}_\mathrm{\tau}\otimes\mathbf{U}_\mathrm{c})^T,$$where subscript (1) denotes mode-1 unfolding, $$$\mathbf{C}_{(1)}$$$ is the unfolded core tensor, and each $$$\mathbf{U}$$$ contains basis functions for the corresponding tensor dimension.

Pulse Sequence

We employ an ECG-free continuous-acquisition SR-FLASH prototype pulse sequence which collects readouts throughout the entire SR period. Stack-of-stars acquisition was implemented with golden-angle ordering in-plane and variable-density Gaussian random sampling for $$$k_z$$$. Training data (the 0° spoke at $$$k_z=0$$$) were collected every fourth readout.

Image Reconstruction

To calculate $$$M$$$, we first obtained a “real-time” reconstruction $$$\tilde{I}(\mathbf{x},t)=I(\mathbf{x},c(t),\tau(t),h(t))$$$ with only one time dimension (elapsed time $$$t$$$) depicting a mixture of motion, T1 recovery, and dynamic contrast enhancement (DCE). This reconstruction was calculated from$$\mathbf{\tilde{U}_x}=\arg\min_{\mathbf{U}}\|\mathbf{d}-E(\mathbf{U\tilde{\Phi}})\|_2^2,$$where $$$\mathbf{d}$$$ is measured data, $$$E(\cdot)$$$ describes multichannel MR encoding/undersampling, and $$$\tilde{\mathbf{\Phi}}$$$ contains real-time basis functions from the singular value decomposition (SVD) of the training data. Systolic images from each heartbeat were extracted from $$$\mathbf{\tilde{A}=\tilde{U}_x\tilde{\Phi}}$$$; translational motion was estimated by registering each systolic image to the systolic image from the last heartbeat, maximizing mutual information⁴ over an automatically selected cardiac region. The measured data were then motion-compensated by applying linear phase modulation in k-space (denoted as $$$\mathbf{M}^{-1}\mathbf{d}$$$).

Following motion compensation, the tensor subspace basis $$$\mathbf{\Phi=C}_{(1)}(\mathbf{U}_\mathrm{h}\otimes\mathbf{U}_\mathrm{\tau}\otimes\mathbf{U}_\mathrm{c})^T$$$ was estimated via Bloch-constrained low-rank tensor completion¹ of the compensated training data, and the spatial factor $$$\mathbf{U_x}$$$ was recovered as$$\mathbf{U_x}=\arg\min_{\mathbf{U}}\|\mathbf{M}^{-1}\mathbf{d}-E(\mathbf{U\Phi})\|_2^2+\lambda\|\mathbf{\Psi{U}}\|_1,$$where $$$\mathbf{\Psi}$$$ is a sparsifying transform. Fig. 1 depicts an image reconstruction flowchart.

Analysis

To calculate systolic myocardial blood flow (MBF), we fit a time-resolved T1 map $$$T_1(\mathbf{x},h)$$$ at end-systole, which we then used to produce a time-resolved gadolinium concentration map$$Gd(\mathbf{x},h)=\frac{\Delta{R}_1(\mathbf{x},h)}{\gamma}=\frac{\left(\frac{1}{T_1(\mathbf{x},h)}-\frac{1}{T_1(\mathbf{x},0)}\right)}{\gamma},$$where $$$\gamma$$$ is the T1 relaxivity of the contrast agent. Segmentwise Fermi deconvolution⁵ of myocardial Gd concentration by left ventricular Gd concentration yielded MBF.

Imaging Parameters

A total of n=5 healthy volunteers were imaged on a 3T scanner (Biograph mMR, Siemens). Pulse sequence parameters were FA=10°, TR/TE=3.2/1.4ms, FOV=288×288×96mm³, matrix size=144×144×12, spatial resolution=2×2×8mm³. A 0.05mmol/kg dose of Gadavist was administered at rest, at a rate of 4mL/s. The total scan time was 60s. Image reconstruction was performed for 20 cardiac bins and 88 saturation times; $$$\mathbf{\Psi}$$$ was the 4-level 3D symlet-4 wavelet transform⁶.

Results and Discussion

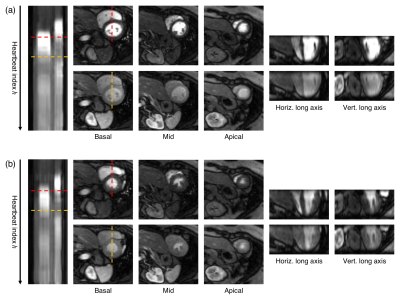
Fig. 2 depicts temporal profiles of a real-time image before and after motion correction. Despite being only a least-squares low-rank reconstruction, the image quality of $$$\tilde{I}(\mathbf{x},t)$$$ is sufficient for image registration. Note that the images being registered are from different saturation times, so T1-weighting is different at each heartbeat. Mutual information cost functions are suitable for multimodal image registration, and can therefore handle the varying T1-weightings.

Example multidimensional perfusion images are shown in Fig. 3. Three short-axis slices, two long-axis reformats, and temporal profiles along $$$h$$$ are shown for both systole and diastole. The images contain little influence from respiratory motion, and clearly depict Gd dynamics.

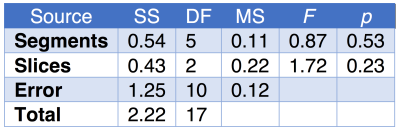
MBF values for one subject were calculated and a two-way ANOVA determined if flow was similar across six segments for each of three slices. Table 1 shows the ANOVA results; no significant differences were found (as expected for a healthy volunteer). The distribution of MBF values was 1.29±0.36mL/g/min, within the reported normal range⁷.

Conclusions

Acknowledgements

References

¹Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Nature Biomed Eng. 2018;2(4):215-226.

²Liang Z-P. Proc IEEE Int Symp Biomed Imaging. 2007:988-991.

³Zhou R, Huang W, Yang Y, Chen X, Weller DS, Kramer CM, Kozerke S, Salerno M. J Cardiovasc Magn Reson. 2018;20(1):6.

⁴Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. IEEE Trans Med Imaging. 1997;16(2):187-98.

⁵Jerosch‐Herold M, Wilke N, Stillman AE, Wilson RF. Med Phys. 1998;25(1):73-84.

⁶Daubechies I. Ten lectures on wavelets. Siam; 1992.

⁷Motwani M, Kidambi A, Uddin A, Sourbron S, Greenwood JP, Plein S. J Cardiovasc Magn Reson. 2015;17(1):4.