Synopsis

Modern magnetic resonance spectroscopic (MRS) pulse sequences frequently overlook the issue of unwanted coherence pathways as source of numerous spectral artifacts. A novel and robust algorithm which only requires the input of the desired coherence pathway was developed to efficiently dephase all unwanted coherence pathways for any MRS pulse sequence. Experiments were performed on phantoms and healthy volunteers comparing crusher schemes obtained from the literature with those obtained from the optimization algorithm for sLASER and MEGA-sLASER. The results demonstrate that the effects of unwanted coherences can be drastically reduced through the implementation of an optimized crusher and phase cycling scheme.

Introduction

Methods

Phase cycling consists of averaging the measured signals from $$$N_p$$$ repetitions of an experiment where the phases of the RF pulses and receiver are varied in order for the desired pathways to constructively interfere and undesired pathways cancel. This can be done in two different ways. The first, referred to as nested schemes, consists of varying the phase of a single RF pulse from one repetition to the next, which is what is typically implemented in MRS. The second way is referred to as cogwheel phase cycling⁷, and consists of varying the phase of several of the RF pulses simultaneously from one cycle to another, which has not yet been implemented in in vivo MRS. Both methods dephase UCPs through the same mechanism and can be understood by considering coherence pathways. For a given coherence pathway, $$$\boldsymbol{\rho}$$$, the phase of the measured signal is given by^7,8

^{$$ \Phi^{(m)}(\boldsymbol{ \rho }) = \sum_{i=1}^{N_{RF}}\phi_i^{(m)}\Delta\rho_i + \phi_{rec}^{(m)} ,$$}

where $$$\Delta\rho_i$$$ indicates the change in coherence order induced by the i^th RF pulse, $$$\phi_i^{m}$$$ is the phase of the i^th RF pulse for cycle $$$m$$$, and $$$\phi_{rec}^{(m)}$$$ is the receiver phase for cycle $$$m$$$. Constructive interference is obtained when^7,8

$$N_p^{-1}\sum_{m=1}^{N_{p}}exp[-\Phi^{(m)}(\boldsymbol{\rho})] = 1. $$

The optimal phase cycling scheme in the new DOTCOPS algorithm is obtained by determining all possible phase cycling schemes considering both nested and cogwheel schemes and selects the scheme which dephases the largest number of UCPs. The optimal crusher scheme is then obtained by using the original DOTCOPS algorithm^6,9 but only considering coherence pathways which have not been dephased by phase cycling. The new DOTCOPS algorithm was run choosing an 8-step phase cycle for five MRS sequences, although it can handle any $$$N_p$$$.

DOTCOPS without phase cycling optimization was compared in phantoms and in vivo for the pulse sequences sLASER and MEGA-sLASER, with full experimental details available in a previous manuscript⁹. Crusher schemes from literature for sLASER and MEGA-sLASER were from Scheenen et al.¹⁰ and Andreychenko et al.³, respectively. For the MEGA-sLASER experiments the residual water signal, which originates from UCPs, was quantified by integrating the magnitude signal from 4.4 to 5.0 ppm and normalizing relative to the water signal from the literature scheme.

Results and Discussion

The inclusion of an optimized 8-step phase cycling scheme can reduce the effective crushing strength for a 9-pulse experiment by approximately a factor of two, as the minimum crushing strength with DOTCOPS without phase cycling⁹ was 1.00, whereas with phase cycling it is 1.97 (Table 1). It was found that cogwheel phase cycling outperformed nested phase cycling for all sequences.

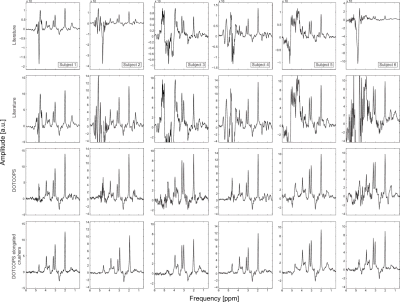
There is substantial baseline distortion in phantom experiments with the literature crusher scheme for sLASER which can be eliminated through the use of the DOTCOPS crusher scheme (Figure 1), whereas for MEGA-sLASER there is severe water contamination and spurious echoes which can also be rectified with DOTCOPS (Figure 2). In vivo spectra from sLASER contain UCPs which are so severe they completely obscure the spectra, which are virtually eliminated with DOTCOPS to produce high-quality spectra (Figure 3). Similarly, the measured in vivo spectra for MEGA-sLASER with the literature crusher scheme shows strong spurious echo signals and uncrushed residual water, whereas the DOTCOPS scheme can greatly reduce the spurious echoes and uncrushed water without changing the gradient durations (Figure 4). Furthermore, the DOTCOPS scheme which uses crusher durations matched to the inter-pulse delays further reduces the uncrushed water signal (Figure 4). The quantified residual water showed a decrease of 56% to 99% and 81% to 99% for DOTCOPS and DOTCOPS elongated crusher schemes over the literature scheme, respectively.

Conclusion

Acknowledgements

References

1. Garwood, M. & DelaBarre, L. The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR. Jour Magn Reson 153, 155–177 (2001).
2. Scheenen, T. W., Heerschap, A. & Klomp, D. W. Towards 1H-MRSI of the human brain at 7T with slice-selective adiabatic refocusing pulses. Magn Reson Mater Phy 21, 95–101 (2008).
3. Andreychenko, A., Boer, V. O., Arteaga de Castro, C. S., Luijten, P. R. & Klomp, D. W. J. Efficient Spectral Editing at 7 T: GABA Detection with MEGA-sLASER. Magn Reson Med 68, 1018–1025 (2012).
4. Haase, A., Frahm, J., Matthaei, D., Hanicke, W., Bomsdorf, H., Dietmar, K., Tischler, R. MR imaging using stimulated echoes (STEAM). Radiology 160, 787–790 (1986).
5. Bottomley, P. A. Spatial Localization in NMR Spectroscopy in Vivo. Ann N Y Acad Sci 508, 333–348 (1987).
6. Landheer, K. & Juchem, C. Optimized Crusher Design for Magnetic Resonance Spectroscopy. 2017 Proc ISMRM Program Number 1288.
7. Levitt, M. H., Madhu, P. K. & Hughes, C. E. Cogwheel phase cycling. Jour Magn Reson 155, 300–306 (2002).
8. Malom H. Levitt. Spin Dynamics. (Wiley, 2008).
9. Landheer, K. & Juchem, C. Dephasing Optimization Through Coherence Order Pathway Selection (DOTCOPS) for Improved Crusher Schemes in Magnetic Resonance Spectroscopy. Magn Reson Med [Epub ahead of print] (2018).
10. Scheenen, T. W. J., Klomp, D. W. J., Wijnen, J. P. & Heerschap, A. Short echo time 1H-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magn Reson Med 59, 1–6 (2008).