Synopsis

In this work, a fast and flexible TOF technique is proposed by applying sliding-slice spiral acquisition with localized quadratic encoding RF pulse. Due to the fast acquisition, water-fat separation and deblurring can also be applied using data from two TEs to improve the visualization over the conventional out of phase method. Volunteer scans in head and neck have demonstrated that the proposed method is 0.4 - 2 times faster than the conventional 2D Cartesian TOF and 3D Cartesian multi-slab TOF, yet provides slightly better visibility of the flow.

Introduction

Theory

Localized Quadratic Encoding

In LQ encoding, a frequency modulated (FM) RF pulse excites a slab. Let γ be the gyromagnetic ratio, G be the slice selection gradient, and δ be the target slice thickness, then the FM RF pulse has a duration of $$$τ=\frac{1}{γGδ}$$$ and gives a quadratic phase as²

$$b_{1}(t)=β_{1}e^{jπM(\frac{t}{τ})^{2}}, |t|<0.5τ. (1)$$

β₁ is a constant magnitude with respect to t. The parameter M is referred to as the time-band-width product of the RF pulse, and also gives the ratio of the excited slab width to the final reconstructed slice resolution. During the acquisition, a series of slabs are overlapped with the center-to-center spacing between the adjacent slabs being δ. Images with slice resolution δ can then be reconstructed by removing the predetermined quadratic phase in the Fourier domain of the slice dimension. The signal-to-noise ratio (SNR) of the reconstructed images is proportional to $$$\sqrt{M}$$$.

Sliding-slice Spiral Acquisition

When the sliding-slice spiral acquisition⁴ is applied to LQ encoding, the slab location is advanced by a step of $$$\frac{δ}{b}$$$ as the index of the spiral interleaf increases, where b is the number of spiral interleaves in one slab. With this approach, the start-up cycles used to achieve the steady-state for each slice can be eliminated. A simple linear phase is applied in the Fourier domain of the slice dimension to reconstruct the images.

Methods

Data Acquisition

TOF data with three volunteers were collected on a 3T Philips Ingenia scanner with a 17-channel head and neck coil. For all fully sampled spiral scans, data were acquired at two TEs with ΔTE = 1.15 ms. The field maps of the static field inhomogeneity were obtained from separate low-resolution Cartesian scans. Conventional Cartesian 3D multi-slab TOF and 2D multi slice TOF were also performed, both with a 63% partial echo acquisition. A venous saturation pulse was performed in each scan. Flow compensation gradients were applied unless stated otherwise.

Reconstruction

Before the general spiral reconstruction, phase corrections for the sliding-slice and LQ encoding were performed. Water only images were obtained by using a joint water-fat separation and deblurring method ⁵. Images at TE = 3.5 ms were also deblurred to obtain the out-of-phase images for comparison.

Results and Discussion

Figure 1(a) shows that the adjacent fat can blur into the vessels as pointed by the yellow arrows in the out-of-phase image. Therefore, the signal of the blood vessels can appear narrower and less uniform compared to the water only image (figure 1(b)). This is also evident in the axial maximum intensity projection (MIP) images shown in figure 2. However, the extent of the artefacts from the blurred fat would also be affected by the contrast between the flow and the static tissue.­­­­­­

A smaller value for M with a larger flip angle is similar to a 2D scan, leading to better flow contrast and better sensitivity to slow perpendicular flow, while a larger value for M with a smaller flip angle is similar to a 3D scan, yielding more uniform flow in all directions as demonstrated in figure 3.

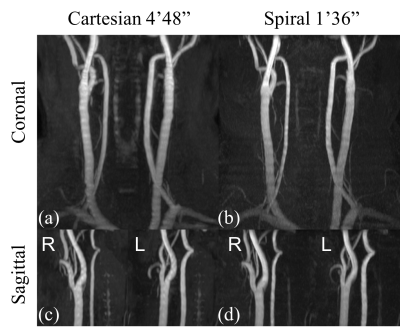
A value of M =16 was used in magnetic resonance angiography (MRA) near the circle of Willis. The result from the proposed method has slightly better visibility of the flow compared to the Cartesian reference as pointed by the yellow arrows in figure 4, possibly due to the elimination of fat and the thinner slab. A smaller M was used in neck MRA. The MIP images appear sharper compared to the 2D Cartesian TOF with overlapping thicker slices (figure 5). Sliding-slice acquisition reduces the scan time by 20-26% in these examples. The proposed method is two times faster than the 2D Cartesian scan and 40% faster than the 3D Cartesian scan that has a SENSE factor of 3. It will also be about 50% faster than the 3D multi-slab Dixon spiral TOF⁶ with the same readout length and the same number of TEs.

Conclusion

Acknowledgements

References

1. Pipe JG. Spatial Encoding and reconstruction in MRI with quadratic phase profiles. Magn Reson Med. 1995;33:24- 33.

2. Pipe JG. Analysis of localized quadratic encoding and reconstruction. Magn Reson Med. 1996;36:137- 146.

3. Pipe JG. Flow effects in localized quadratic, partial Fourier MRA. Magn Reson Med. 1999;41:309- 314.

4. Zwart NR, Pipe JG. Sliding slice 2D spiral time of flight MRA. In Proceedings of the 25th anunual meeting of ISMRM, Honolulu USA, 2017. Abstract 4018.

5. Wang D, Zwart NR, Pipe JG. Joint water-fat separation and deblurring for spiral imaging. Magn Reson Med. 2018;79:3218- 3228.

6. Zwart NR, Wang D, Pipe JG. Spiral time of flight with Dixon water and fat separation. In proceedings of the 24th anunual meeting of ISMRM, Singapore, 2016. Abstract 1834.