0666
Joint recovery of variably accelerated multi-contrast MRI acquisitions via generative adversarial networks1Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2Aysel Sabuncu Brain Research Center, Bilkent University, Ankara, Turkey, 3Neuroscience Graduate Program, Bilkent University, Ankara, Turkey
Synopsis
Two frameworks to recover missing data in accelerated MRI are
Introduction
A common approach to accelerate MRI is to reconstruct undersampled acquisitions1-5. Yet, reconstruction performance diminishes towards higher acceleration factors (Fig. 1a). An alternative framework to recover missing data is synthesis6-8, where a set of missing contrasts is predicted based on a set of acquired contrasts of the same anatomy. However, lack of evidence about the missing contrasts can either lead to synthesis of artificial features or insensitivity to features (Fig. 1a). To address the issues with these two mainstream frameworks, we propose a new approach that synergistically performs reconstruction and synthesis to enable reliable recovery in accelerated MRI (Fig. 1b).Methods
The proposed approach was implemented using generative adversarial networks (GANs)9. A GAN consists of a generator and a discriminator. Given lightly undersampled acquisitions of source contrasts and highly undersampled acquisitions of target contrasts, the generator learns to recover high quality target-contrast images. Meanwhile, the discriminator learns to discriminate between the images recovered by the generator and real images. The generator $$$G$$$ and discriminator $$$D$$$ are trained using an adversarial loss function ($$$\mathcal{L}_{Adv}(\theta_{D},\theta_{G}) $$$):
$$ \mathcal{L}_{Adv}(\theta_{D},\theta_{G})=-E_{{\boldsymbol{m}}}[(D(\boldsymbol{m};\theta_{D})-1) ^{2} ]-E_{\boldsymbol{m^{hu}m^{lu}}}[D(G(\boldsymbol{m^{hu}},\boldsymbol{m^{lu}};\theta_{G});\theta_{D})^2]$$
where $$$\theta_{G}$$$ and $$$\theta_{D}$$$ are the parameters of $$$G$$$ and $$$D$$$ respectively, $$$\boldsymbol{m}$$$ represents the MR images aggregated across $$$n$$$ contrasts $$$(m_{1},m_{2},...,m_{n})$$$ in the training dataset, $$$\boldsymbol{m^{hu}}$$$ represents the heavily undersampled acquisitions aggregated across $$$l$$$ target contrasts $$$(m_{1},m_{2},...,m_{l})$$$, and $$$\boldsymbol{m^{lu}}$$$ represents the lightly undersampled acquisitions aggregated across $$$n-l$$$ source contrasts $$$(m_{l+1},m_{l+2},...,m_{n})$$$. $$$G$$$ is trained to minimize ($$$\mathcal{L}_{Adv}(\theta_{D},\theta_{G}) $$$), and $$$D$$$ is trained to maximize ($$$\mathcal{L}_{Adv}(\theta_{D},\theta_{G}) $$$). To ensure reliable recovery, a pixel-wise loss ($$$\mathcal{L}_{L1}(\theta_{G}) $$$) was also incorporated between the generated and reference images to train the generator:
$$\mathcal{L}_{L1}(\theta_{G})=E_{\boldsymbol{m,m^{hu},m^{lu}}}[ \parallel G(\boldsymbol{m^{hu},m^{lu}};\theta_{G})-\boldsymbol{m}\parallel_{1}]$$
The generator consisted of 3 convolutional layers-9 Resnet blocks-3 convolutional layers, and the discriminator consisted of 4 convolution layers.
We demonstrated the proposed approach on two public datasets. In the IXI dataset, 39 healthy subjects’ T1, T2- and PD-weighted images were analyzed (28 for training, 2 for validation, 9 for testing; 100 cross-sections per subject). In the BRATS dataset, 45 glioma patients’ T1- and T2-weighted images were analyzed (35 for training, 10 for testing; 100 cross-sections per subject). Optimum number of epochs and relative weightings of the loss functions were selected by performing cross-validation on the IXI dataset, and same set of parameters were used for the BRATS dataset. Adam optimizer was used with parameters $$$\beta1$$$=0.5, $$$\beta2$$$=0.999, and dropout regularization was used with a dropout rate of 0.5.
We compared the proposed rsGAN method against two architectures: a reconstruction network (rGAN) that recovers target-contrast images based on undersampled acquisitions of the target contrast, and a synthesis network (sGAN) that synthesizes target-contrast images based on fully sampled source-contrast images.
Results
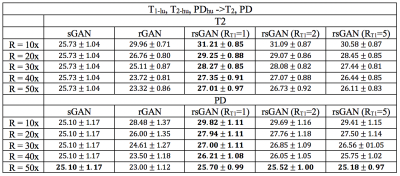
Table I lists peak SNR (PSNR) values for recovered T2- and PD-weighted images across the test subjects in the IXI dataset. T1-weighted images were taken as source contrast (RT1=1x, 2x, 5x undersampled), and T2- and PD-weighted images were taken as target contrasts (R=10x, 20x, 30x, 40x, 50x). In T2 recovery, on average, rsGAN (RT1=1x) achieves 2.84±1.01 dB higher PSNR than rGAN, and 2.88±1.69 dB higher PSNR than sGAN. In PD recovery, rsGAN (RT1=1x) achieves 2.22±0.58 dB higher PSNR than rGAN, and 2.23±1.63 dB higher PSNR than sGAN.
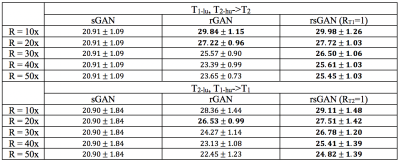
Table II lists PSNR values for recovered T1- and T2-weighted images across the test subjects in the BRATS dataset. T1- or T2-weighted images were taken as source contrasts (R=1x), and T1- or T2-weighted images were taken as target contrasts (R=10x, 20x, 30x, 40x, 50x). In T1 recovery, rsGAN achieves 1.12±0.87 dB higher PSNR than rGAN, and 6.14±1.87 higher PSNR than sGAN. In T2 recovery, rsGAN achieves 1.78±0.84 dB higher PSNR than rGAN, and 5.83±1.71 dB higher PSNR than sGAN.
Representative T2- and PD-weighted images in IXI recovered by sGAN, rGAN, and rsGAN are shown in Fig. 2. Representative T1- and T2-weighted images in BRATS recovered by sGAN, rGAN, and rsGAN are shown in Fig. 3. rGAN suffers from loss of intermediate spatial frequency content due to lack of evidence in the target contrast, and sGAN suffers from synthesis of artificial pathology or failure to synthesize existing pathology. On the other hand, rsGAN enables reliable recovery of the target contrasts by relying on information from both source and target contrasts.
Discussion
Here, we proposed a new approach that performs synergistic reconstruction and synthesis to accelerate multi-contrast MRI. The proposed method preserves intermediate spatial frequency details by relying on the lightly undersampled source contrasts. Meanwhile, it prevents feature loss or synthesis of artificial features by relying on heavily undersampled acquisitions of the target contrast.Conclusion
The proposed approach enables reliable recovery of missing data in variably undersampled multi-contrast MRI acquisitions, by effectively combining information from source and target contrasts.Acknowledgements
This work was supported in part by a Marie Curie Actions Career Integration Grant (PCIG13-GA-2013-618101), by a European Molecular Biology Organization Installation Grant (IG 3028), by a TUBA GEBIP 2015 fellowship, by a Tubitak 1001 Grant (117E171) and by a BAGEP 2017 fellowship.
References
1. Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: IEEE 13th International Symposium on Biomedical Imaging (ISBI). ; 2016. pp. 514–517.
2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–1195.
3. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med. 2018;79:3055–3071.
4. Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Neural Networks for Compressive Sensing (GANCS) MRI. IEEE Trans. Med. Imaging 2018:1–1.
5. Schlemper J, Caballero J, Hajnal J V., Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction. In: Springer, Cham; 2017. pp. 647–658.
6. Dar SUH, Yurt M, Karacan L, Erdem A, Erdem E, Çukur T. Image Synthesis in Multi-Contrast MRI with Conditional Generative Adversarial Networks. arXiv Prepr. 2018.
7. Jog A, Carass A, Roy S, Pham DL, Prince JL. Random forest regression for magnetic resonance image synthesis. Med. Image Anal. 2017;35:475–488.
8. Chartsias A, Joyce T, Giuffrida MV, Tsaftaris SA. Multimodal MR Synthesis via Modality-Invariant Latent Representation. IEEE Trans. Med. Imaging 2018;37:803–814.
9. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks. In: Advances in Neural Information Processing Systems. ; 2014. pp. 2672–2680.
Figures