0663
Accelerated MRI Using Residual RAKI: Scan-specific Learning of Reconstruction Artifacts1Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Computer Assisted Clinical Medicine, University Medical Center Mannheim, Heidelberg University, Mannheim, Germany
Synopsis
Recently, there has been an interest in machine learning reconstruction techniques for accelerated MRI, where the focus has been on training regularizers on large databases. Another line of work, called Robust Artificial-neural-networks for k-space Interpolation (RAKI) explored the use of CNNs, trained on subject-specific ACS data for improving parallel imaging. In this work, we propose a ResNet architecture, called Residual RAKI (rRAKI) for training a subject-specific CNN that simultaneously approximates a linear convolutional operator and a nonlinear component that compensates for noise amplification artifacts that arise from coil geometry. Brain data shows improved noise resilience at high acceleration rates.
Introduction
Accelerated imaging is frequently used in clinical MRI, by means of parallel imaging techniques. GRAPPA is one such method that performs linear interpolation in k-space using convolutional kernels, estimated from autocalibration signal (ACS).1 Alternative accelerated reconstruction methods based on machine learning (ML) have recently received interest, with a focus on generating advanced regularizers trained on large databases of MR images.2-9 In another line of work, called Robust Artificial-neural-networks for k-space Interpolation (RAKI), a nonlinear k-space interpolation method was proposed.10 This method uses subject-specific convolutional neural networks (CNNs) trained on ACS data, and showed improvement in terms of noise resilience over GRAPPA. However, linear interpolation holds advantages, such as requiring fewer ACS data. In this study, we propose a residual CNN architecture (ResNet),11 called residual RAKI (rRAKI), to combine advantages of both linear GRAPPA and non-linear RAKI reconstructions. The proposed residual CNN consists of a linear residual connection, which implements a convolution that estimates most of the energy in k-space, and a multi-layer network with non-linear activation functions that estimates the imperfections, such as noise amplification due to coil geometry that arises from the linear component.Methods
rRAKI Architecture: Figure 1 depicts the CNN architecture for rRAKI for uniformly undersampled k-space data. The network takes an input of all sampled data across all coils (2nc input channels, nc: number of coils, factor 2: mapping complex k-space to real field) and output all the missing lines for a given coil, as in RAKI.10 The residual connection, implements a linear reconstruction based on shift-invariant k-space convolution, which is denoted by Gc. The multi-layer feedforward network for estimating the artifacts uses a 3-layer architecture, similar to RAKI, which is denoted by Fc. The final reconstruction result combines these two components, as
$$ R^c(x) = F^c(x) + G^c(x)$$
This network is trained end-to-end on the subject-specific ACS data using the following objective function:
$$ min \ ||s(x) - R^c(x)||^2_2 + \lambda||s(x) - G^c(x)||^2_2 $$
where s(x) are the target k-space points in the ACS data, which is generated similar to GRAPPA reconstruction, $$$G^c(x) = w^c_g * x$$$ is a convolution, $$$F^c(x) = F^c_3(F^c_2(F^c_1(x)))$$$ is a 3-layer network with $$$F^c_1(x) = ReLU(w^c_1 * x)$$$, $$$F^c_2(x) = ReLU(w^c_2 * x)$$$, $$$F^c_3(x) = w^c_3 * x$$$. λ creates a weighting between two components, and for this study, λ=1 was used.
In Vivo Imaging: Brain imaging was performed at 3T and 7T. 3D-MPRAGE was acquired at 3T, with FOV=224×224×179mm3, resolution=0.7×0.7×0.7mm3, R=2 (retrospectively undersampled to R=4,6), and R=5. 3D-MPRAGE was also acquired at 7T, with FOV=230×230×154mm3, resolution=0.6×0.6×0.6mm3, R=4,5,6. R=5,6 were acquired with two averages to reduce SNR penalty. Functional MRI was acquired at 3T with TE/TR=37/800ms, 2mm isotropic resolution, simultaneous multi-slice (SMS) R=16, and blipped-CAIPI with FOV/3. SMS data was processed using readout concatenation.12
Results
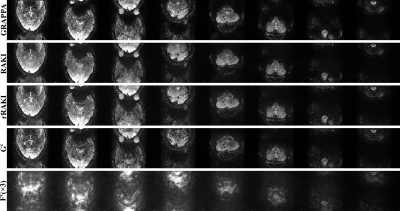
Figure 2 shows the results of the MPRAGE scan at 3T. Compared to GRAPPA, rRAKI shows better noise resilience, similar to RAKI. Furthermore, the nonlinear component, Fc component of the output only captures noise amplification consistent with coil geometry. A similar trend is observed in Figure 3 at 7T, with no visual blurring at this high resolution. Figure 4 and 5 show sets of 8 slices from fMRI data at SMS16. At this high SMS acceleration rate, rRAKI outperforms RO-SENSE-GRAPPA in terms of noise resilience and RAKI in terms of blurring artifacts. Note Fc component captures more than just noise in this case, due to the imperfections in the EPI-based ACS data for this application.Discussion
In this work, we formulated ResNet architecture for interpolation of missing k-space lines using both linear and non-linear components. Importantly, both these components are trained only on subject-specific ACS data, without requiring a database of images. Our proposed method, rRAKI, offered better noise resilience compared to GRAPPA, and fewer blurring artifacts compared to RAKI. Furthermore, the proposed training provides flexibility for different weights on linear and non-linear components. ResNet architectures have shown advantages in other applications, including accelerated convergence and hypothesized easier optimization of the residual mapping, which was also observed in this study. In this work, we jointly trained the linear convolutional kernel and the nonlinear component. While an explicit GRAPPA kernel may be used to define the residual at the output, without a residual connection in the CNN, in our experience, this leads to convergence to local minima, even with a batch normalization layer.Conclusion
The proposed residual RAKI uses scan-specific CNNs trained on limited ACS data to learn reconstruction artifacts in addition to a linear reconstruction, and improves upon other k-space interpolation-based methods.Acknowledgements
Grant support: NIH R00HL111410, NIH P41EB015894, NIH U01EB025144, and NSF CAREER CCF-1651825.References
1. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002 Jun;47(6):1202-1210.
2. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. Proc ISBI 2016 pp. 514-517.
3. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018 Jun;79(6):3055-3071.
4. Lee D, Yoo J, Tak S, Ye JC. Deep Residual Learning for Accelerated MRI using Magnitude and Phase Networks. IEEE Trans Biomed Eng. 2018(65): 1985-1995.
5. Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection‐reconstruction MR. Magn Reson Med. 2018 Sep;80(3):1189-1205.
6. Aggarwal HK, Mani MP, Jacob M. MoDL: Model Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging, doi: 10.1109/TMI.2018.2865356, 2018.
7. C.Qin C, Hajnal JV, Rueckert D, Schlemper J, Caballero J, Price AN. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging, doi: 10.1109/TMI.2018.2863670, 2018.
8. Kwon K, Kim D, Park H. A parallel MR imaging method using multilayer perceptron. Med Phys, vol. 44, pp. 6209–6224, 2017.
9. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging, vol. 37, pp. 491–503, 2018.
10. Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific Robust Artificial-neural-networks for k-space Interpolation (RAKI) Reconstruction: Database-free Deep Learning for Fast Imaging. Magn Reson Med. doi: 10.1002/mrm.27420, 2018.
11. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Proc CVPR 2016. pp. 770-778.
12. Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K. Multiband multislice GE‐EPI at 7 tesla, with 16‐fold acceleration using partial parallel imaging with application to high spatial and temporal whole‐brain fMRI. Magn Reson Med. 2010 May;63(5):1144-53.
Figures




Reconstruction results of SMS=16 fMRI data, showing the first 8 slices. GRAPPA kernel size is 7×6, RAKI and rRAKI kernel sizes are as in Figure 2. rRAKI outperforms both GRAPPA and RAKI in terms of noise amplification and blurring artifacts respectively. Due to the imperfections in the EPI-based ACS data for this SMS reconstruction, Fc component includes ghosting artifacts as well, capturing more than just noise amplification.