Synopsis

Axon diameter mapping using diffusion MRI in the rat corpus callosum was validated using confocal microscopy with a staining for neurofilaments. When confounding factors such as extra-axonal water and dispersion are addressed, the effective MR axon radii are in good quantitative agreement with histology. However, using MRI, we are limited to the estimation of a single metric representing the entire distribution, which has shown to be dominantly sensitive to the largest axons in the voxel volume of interest.

Introduction

Axon diameter mapping using diffusion MRI (dMRI) has been a highly debated topic of research^1,2. Discrepancies between histology and dMRI-derived axon diameters uncovered various confounding factors, e.g. dispersion³, time-dependent extra-axonal diffusion^4-7, reduced signal attenuation due to long diffusion gradient durations^8,9, and/or tissue shrinkage². Hardware developments and following insights in biophysical modeling promote the revival of MR axon diameter mapping. In particular, dMRI can become (a) specific to intra-axonal signal in a high $$$b$$$ regime because the extra-axonal signal decays exponentially fast¹⁰; and (b) predominantly sensitive to the largest axons⁴ of the underlying distribution because of a volume correction^4,11 and the $$$r^4$$$-scaling of the radial signal attenuation of restricted diffusion inside a cylinder of radius⁵ $$$r$$$ when approaching the Neuman’s limit⁹. A previous study¹² measured human axon radii by evaluating the signal scaling in an axon-specific $$$b$$$-regime. The in vivo MR results were in good agreement with histological values reported in literature^13,14 after accounting for the tail-weighting. Here, we validate the technique by comparing the MR-derived axon diameters directly to confocal microscopy.

Theory

In the absence of any extra-axonal signal, the powder-averaged diffusion-weighted signal decays as $$\bar{S}(b)\,=\,e^{-bD_a^\perp}\frac{\sqrt{\pi}}{2}\frac{f}{\sqrt{D_a^\parallel}}\,b^{-1/2}\,+\gamma,$$

with $$$\gamma$$$ a still water signal fraction¹⁵, $$$f$$$ the intra-axonal signal fraction, and $$$D_a^\perp$$$ and $$$D_a^\parallel$$$ the intra-axonal radial and axial diffusivities, respectively. In each voxel, $$$D_a^\perp$$$ projects the axon radius distribution $$$P(r)$$$ onto a scalar “effective” radius^4,12 through the volume correction¹¹ and a model of restricted diffusion inside a cylinder⁵: $$r_\textrm{eff}\equiv\sqrt[4]{\langle\,r^6\,\rangle\,/\,\langle\,r^2\,\rangle}.$$

The intra-axonal parallel diffusivity¹⁶ serves here as a proxy for the intrinsic diffusivity $$$D_0$$$.

Methods

Samples: Animal experiments, preapproved by the institutional and national authorities, were carried out according to European Directive 2010/63. Three Long Evans rats (Female, 12-weeks-old) were transcardially perfused using 4% paraformaldehyde. The extracted brains were kept 24$$$h$$$ in 4% paraformaldehyde and washed out using PBS during two days (changed daily).

MRI: The samples were scanned on an 16.4T MR scanner (Bruker BioSpin) with $$$\Delta/\delta\,=\,20/7.1\,\mathrm{ms}$$$ interfaced with an AVANCE IIIHD console and a micro2.5 imaging probe with maximal gradient amplitude $$$G\,=\,1500\,\mathrm{mT/m}$$$. Diffusion-weighting was applied using a RARE sequence in the midsagittal plane along 60 gradient directions for a densely sampled spectrum of $$$b$$$-values up to $$$100\,\mathrm{ms/\mu\,m^2}$$$. Furthermore, $$$\mathrm{TR/TE}\,=2400/30.4\,\mathrm{ms}$$$ and the spatial resolution was $$$100\,\times\,100\times\,850\,\mathrm{\mu\,m}^3$$$. The spherically-averaged signals were estimated per $$$b$$$-value using a Rician maximum likelihood estimator of the spherical harmonic coefficients. We subtracted the independently estimated (cf. Ref. 17) $$$\gamma$$$ to isolate the intra-axonal signal.

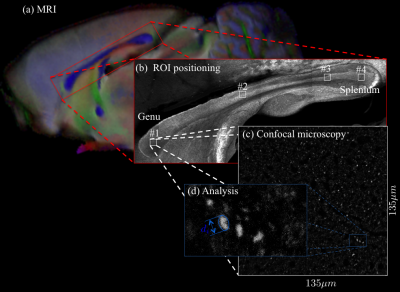
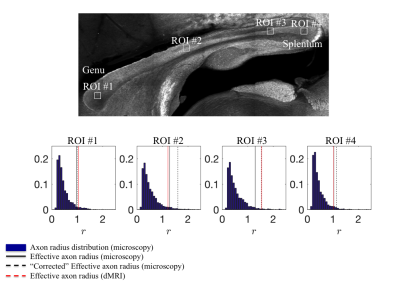
Microscopy: A Zeiss LSM 710 laser scanning confocal microscope was used for immunohistochemistry image acquisition. A tile scan using a 10 objective (EC Plan Neofluar, numerical aperture$$$\,=\,0.3,$$$ Zeiss, Germany) was used to cover the Corpus Callosum (CC) (Fig. 1(b)). Afterwards, 4 ROIs were imaged using a 63 immersion objective (Plan Apochromat, numerical aperture$$$\,=\,1.4$$$, Zeiss, Germany) in confocal mode, with spatial resolution of $$$65\times\,65\times\,150\mathrm{nm^3}$$$ and field-of-view of $$$135\times\,135\mu\,m^2$$$ (Fig. 1(c)). Axons were identified using a neurofilament staining. The long axes of fitted ellipsoids served as proxies for the respective axon diameters.

Results

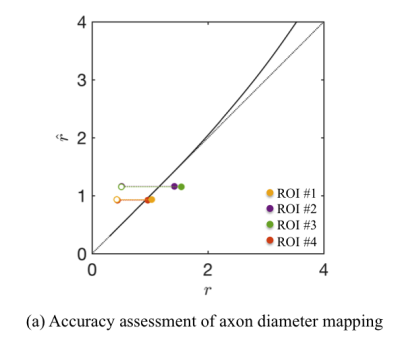
Accuracy assessment: The accuracy of the axon diameter mapping is computed as a function of $$$r$$$ and for the axon radius distributions extracted from histology (Fig.$$$\,5$$$) using a simulation framework using the matrix formalism for diffusion signal attenuation within fully restricted cylinders with our sequence timings18 (Fig.$$$\,2$$$). Errors $$$<25\%$$$ for large $$$r$$$ that are associated to the missing higher-order terms in Van Gelderen’s model set an upper bound on the achievable accuracy.

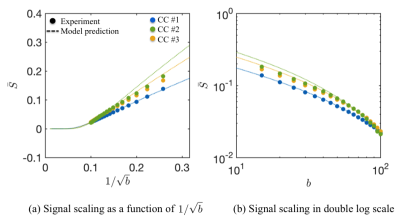
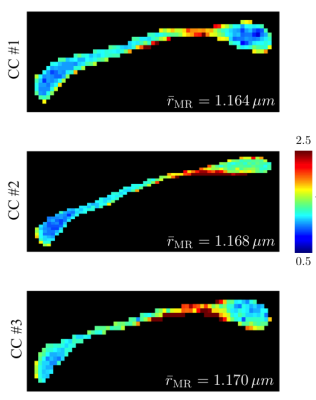
Experimental validation of axon diameter mapping: A visual assessment of the CC-averaged signal decays in all three samples highlight the apparent deviations from the power law scaling, thereby demonstrating sensitivity of dMRI signals to the radial intra-axonal signal in this experimental regime (Fig.$$$\,3$$$). The CC-averaged effective MR radii are highly consistent across all samples ($$$\hat{r}_\textrm{eff}$$$ in Fig.$$$\,4$$$), with the maps being in good agreement with previously reported trends of larger axons in the body of the CC in comparison to the genu and splenium (Fig.$$$\,4$$$). Mesoscopic fluctuations dominate the inter-subject variability. The quantitative comparison of the MR- and microscopy-derived effective radii in four locations of the CC shows differences up to $$$20\%$$$, in agreement with the accuracy assessment of the simulations (Fig.$$$\,5$$$).

Discussion

Acknowledgements

References

1. A. Horowitz, D. Barazany, I. Tavor, M. Bernstein, G. Yovel, and Y. Assaf, “In vivo correlation between axon diameter and conduc- tion velocity in the human brain,” Brain Structure and Function 220, 1777–1788 (2015).
2. G. Innocenti, R. Caminiti, and F. Aboitiz, “Comments on the paper by Horowitz et al.(2014),” Brain structure and function 220, 1789– 1790 (2015).
3. I. Drobnjak, H. Zhang, A. Ianuş,, E. Kaden and D.C. Alexander. “PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study”. Magnetic resonance in medicine 75(2), 688-700 (2016).
4. L. M. Burcaw, E. Fieremans, and D. S. Novikov, “Mesoscopic structure of neuronal tracts from time-dependent diffusion,” NeuroImage 114, 18–37 (2015).
5. H.H. Lee, E. Fieremans, and D.S. Novikov, “What dominates the time dependence of diffusion transverse to axons: Intra-or extra-axonal water?”, NeuroImage 182, 500-510 (2018)
6. S. De Santis, D.K. Jones, and A. Roebroeck, “Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter”, NeuroImage 130, 91-103 (2016)
7. E. Fieremans, L.M. Burcaw, H.H. Lee, G. Lemberskiy, J. Veraart, D.S. Novikov, “In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter”, NeuroImage 129, 414-427 (2016).
8. P. van Gelderen, D. DesPres, P. van Zijl, and C. Moonen, “Evaluation of restricted diffusion in cylinders. phosphocreatine in rabbit leg muscle,” Journal of Magnetic Resonance, Series B 103, 255–260 (1994).
9. C. Neuman. Spin echo of spins diffusing in a bounded medium. The Journal of Chemical Physics, 60(11):4508–4511 (1974)
10. J. Veraart, E. Fieremans, D.S. Novikov, “On the scaling behavior of water diffusion in human brain white matter”, NeuroImage, DOI: 10.1016/j.neuroimage.2018.09.075
11. D. C. Alexander, P. L. Hubbard, M. G. Hall, E. A. Moore, M. Ptito, G. J. Parker, and T. B. Dyrby, “Orientationally invariant indices of axon diameter and density from diffusion MRI,” Neuroimage 52, 1374–1389 (2010).
12. J. Veraart, E. Fieremans, U. Rudrapatna, D.K. Jones, D.S. Novikov, “Breaking the power law scaling of the dMRI signal on the Connectom scanner reveals its sensitivity to axon diameters”, ISMRM 26, 252 (2018)
13. F. Aboitiz, A. B. Scheibel, R. S. Fisher, and E. Zaidel, “Fiber com- position of the human corpus callosum,” Brain research 598, 143– 153 (1992).
14. R. Caminiti, H. Ghaziri, R. Galuske, P. R. Hof, and G. M. Innocenti, “Evolution amplified processing with temporally dispersed slow neuronal connectivity in primates,” Proceedings of the National Academy of Sciences 106, 19551–19556 (2009).
15. G.J. Stanisz, G.A. Wrigth, R.M. Henkelman, and A. Zsafer, “An analytical model of restricted diffusion in bovine optic nerve”, Magnetic Resonance in Medicine 37(1), 103-111 (1997)
16. D.S. Novikov, J. Veraart, I.O. Jelescu, E. Fieremans. “Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI”. Neuroimage 174: 518-538 (2018).
17. B. Dhital, E. Kellner, V.G. Kiselev, and M. Reisert, “The absence of restricted water pool in brain white matter”. NeuroImage 182:398-406 (2018)
18. I. Drobnjak, B. Siow, D.C. Alexander. “Optimizing gradient waveforms for microstructure sensitivity in diffusion weighted MR.” Journal of Magnetic Resonance 206(1):41–51 (2010).