0478
A Variational Neural Network for Accelerating Free-breathing Whole-Heart Coronary MR Angiography1School of Biomedical Engineering & Imaging Sciences, King's College London, London, United Kingdom
Synopsis
3D whole-heart coronary MR angiography (CMRA) has shown great potential to visualize the coronary arteries. However, scan times remain lengthy as a large amount of data needs to be acquired to obtain high-resolution images. Several undersampled compressed-sensing (CS) reconstruction approaches have been applied to accelerate CMRA. However, CS-based techniques suffer from residual aliasing artifacts, high-dependency on regularization parameters and long reconstruction times. We propose a Variational Neural Network for fast reconstruction of undersampled motion-compensated 3D cardiac MRI, which combined with 100% respiratory efficiency, enables the acquisition of high-quality isotropic CMRA images in ~2-4 minutes, and their reconstruction in ~20 seconds.
Introduction
Free-breathing coronary MR angiography (CMRA) has shown significant potential to noninvasively visualize the coronary arteries. 3D whole-heart CMRA, however, remains lengthy, as a large amount of data needs to be acquired to obtain images with adequate spatial resolution for quantification of luminal stenosis. Undersampled acquisitions using compressed sensing (CS) reconstruction have been shown to accelerate CMRA1-2. For high acceleration factors, however, CS-based techniques suffer from residual aliasing artifacts, which may compromise the diagnostic value of the reconstructed image. Additionally, CS-based reconstructions suffer from high computational costs and require the selection of adequate regularization parameters. In this work, we propose to use a variational neural network (VNN)3 to allow fast reconstruction of 3D high-resolution images from prospectively undersampled translational motion-corrected CMRA data. We combine this approach with 100% respiratory efficiency to enable the acquisition of high-quality 1.2 mm3 isotropic CMRA images in ~2-4 minutes, and their reconstruction in ~20 seconds. All parameters of this formulation, including the reconstruction parameters, are learned during the offline training procedure. The proposed approach is compared with Wavelet-based CS reconstruction4 for undersampling factors of 5x and 7x.Methods
Acquisition: Thirty-one healthy subjects underwent free-breathing 3D CMRA acquisition with variable density spiral-like Cartesian sampling (VD-CASPR2,5) on a 1.5T scanner (Siemens Magnetom-Aera). A 2D image-navigator6 precedes the acquisition of each spiral arm to enable beat-to-beat 2D translational respiratory motion estimation/correction and thus 100% respiratory scan efficiency (Fig.1a). Data were acquired in mid-diastole with an ECG-triggered 3D bSSFP sequence, 18-channel body and 32-channel spine coils, fat-saturation, FOV=320x320x80-120 mm3, TR/TE=3.35/1.47 ms, FA=90°, bandwidth=890 Hz/pixel, T2-preparation duration=40 ms and 1.2mm3 isotropic resolution. Acquisitions were performed fully sampled (all subjects) and with an undersampling factor of 5x (6 subjects) and 7x (5 subjects).
VNN Architecture: The proposed pipeline and structure of the variational neural network is presented in Fig.1. Translational motion compensated undersampled k-space data and coil sensitivity maps are provided as input to the VNN. Following the work on the use of VNN3 for reconstruction of accelerated MRI data, in each of the 8 stages of the network, the initial reconstruction $$$x$$$ is updated according to the following variational scheme:
$$x^{i+1} = x^{i} - \lambda \| E x^{i} - d \|^{2}_{2} - \sum_{n=1}^{N_{\kappa}}\phi^{n,i}(\kappa^{n,i}*x^{i})$$
The first term enforces data consistency to the motion compensated undersampled k-space data $$$d$$$, applying the linear operator $$$E$$$, that combines multiplication with coil sensitivity maps and the forward FFT. The second term, can be considered as a regularization function, at network stage $$$i$$$, that convolves the image $$$x$$$ with $$$N_{\kappa}=24$$$ real-valued 11x11 filter kernels $$$\kappa^{n,i}$$$ and then applies the corresponding differentiable penalty functions $$$\phi^{n,i}$$$. Since the input and output data of the VNN are complex-valued, the network learns a set of filters and activation functions for the absolute images, whereas the phase of the input images is kept fixed. The influence of the first term is controlled via a regularization parameter $$$\lambda$$$. The root mean-squared error was used as loss function.
VNN Training: All parameters of this formulation, including the prior model defined by filter kernels, activation functions and data term weights, are learned during an offline training procedure. The network was trained on 2D magnitude images obtained from retrospectively undersampled 5-fold 3D CMRA data of 20 subjects (6080 images). During the training procedure, the output of the VNN is compared to the corresponding fully sampled reference images. Training is performed with retrospective undersampling data to ensure that the effect of respiratory and cardiac motion in both input and output images is identical.
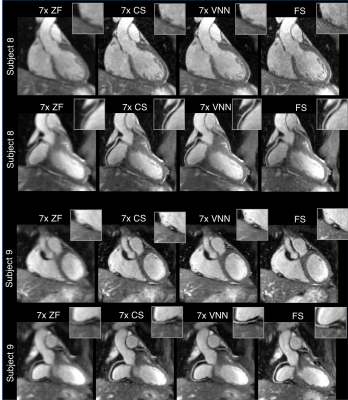
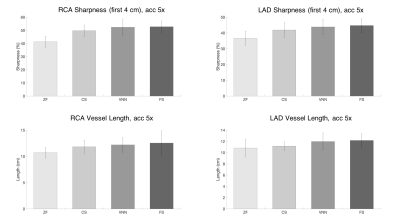
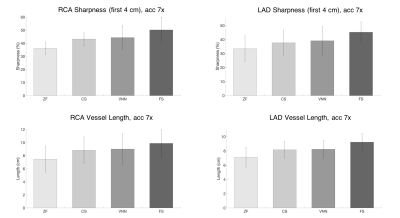
Experiments: Fully-sampled and prospectively undersampled data of 11 healthy subjects (not included in the training) were used to evaluate the framework. The proposed approach was compared to zero-filled (ZF), and Wavelet-based CS reconstructions. Vessel sharpness of the right and left coronary arteries was measured using SoapBubble7.
Results
The average total acquisition time (m:s) was 18:55 for the fully sampled acquisition, 4:11 for an acceleration of 5x and 2:34 for 7x. The proposed framework presents higher image quality than ZF and CS (Fig.2,3), with coronary artery length and sharpness comparable to the fully-sampled reference (Fig.4,5). Average reconstruction time was ~5 minutes for CS and ~20 seconds for the proposed framework.Conclusion
Free-breathing motion-compensated whole-heart 3D coronary images with 1.2mm3 isotropic resolution were successfully obtained using a VNN undersampled reconstruction approach. This approach has shown improved image quality with respect to ZF and CS reconstructions, offering several advantages: i) High-resolution CMRA reconstruction, ii) short scan times leading to reduction of respiratory motion artifacts, iii) no need for tuning of regularization parameters, iv) extremely fast computational time, offering easy integration into clinical workflow.Acknowledgements
This work was supported by EPSRC (EP/P001009, EP/P007619, EP/P032311/1 and Wellcome EPSRC Centre for Medical Engineering (NS/A000049/1).References
1. Akçakaya M, et al. Accelerated isotropic sub-millimeter whole-heart coronary MRI: compressed sensing versus parallel imaging. Magnetic resonance in medicine. 2014;71:815-822.
2. Bustin A, et al. Five‐minute whole‐heart coronary MRA with sub‐millimeter isotropic resolution, 100% respiratory scan efficiency, and 3D‐PROST reconstruction. Magnetic resonance in medicine. 2018; doi: https://doi.org/10.1002/mrm.27354.
3. Hammernik K, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine. 2018;79:3055-3071.
4. Lustig M, et al. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic resonance in medicine. 2007;58(6):1182-1195.
5. Prieto C, et al. Highly efficient respiratory motion compensated free-breathing coronary MRA using golden-step Cartesian acquisition. Journal of magnetic resonance imaging. 2015;41:738-746.
6. Henningsson M, Smink J, Razavi R, Botnar RM. Prospective respiratory motion correction for coronary MR angiography using a 2D image navigator. Magnetic resonance in medicine. 2013;69:486- 494.
7. Etienne A, et al. “Soap-Bubble” visualization and quantitative analysis of 3D coronary magnetic resonance angiograms. Magnetic resonance in medicine. 2002;48:658-66.
Figures

Figure 1: Acquisition: CMRA data were acquired using a 3D variable density undersampled trajectory with spiral profile ordering, preceded by 2D image navigators (iNAV), to enable beat-to-beat 2D translational respiratory motion estimation/correction.
VNN Architecture: Motion-compensated undersampled k-space data and coil sensitivity maps are provided as input to the VNN. Since we are dealing with complex-valued data, the network learns a set of filters and activation functions for the absolute images, whereas the phase is kept fixed. The VNN consists of 8 network stages, each stage presents 24 real-valued 11x11 filters and their corresponding activation functions, resulting in 29192 network parameters.