0233
SMS-MUSSELS: A Navigator-free Reconstruction for Slice-accelerated Multi-shot Diffusion Imaging1University of Iowa, Iowa City, IA, United States, 2GE Healthcare, Milwaukee, WI, United States, 3Stanford University, Stanford, CA, United States
Synopsis
Multi-shot diffusion-weighted (
Introduction
EPI-based diffusion imaging using single-shot readout methods are prone to geometric distortions and blurring, which preclude its utility for high-resolution imaging. Multi-shot diffusion-weighted (msDW) imaging overcomes the above problems by splitting the single long readout into multiple shorter readouts that are acquired over multiple TRs. The shorter k-space readout duration limits the geometric distortions and blurring and achieves a shorter echo-time suitable for high-resolution diffusion imaging. However, the acquisition spanning multiple TRs to cover a single k-space reduce the time efficiency of multi-shot methods. Hence the practical utility of multi-shot methods for high angular resolution studies currently remains limited.
Simultaneous multi-slice1,2 (SMS) imaging acceleration techniques can improve the time efficiency of msDW imaging without sacrificing SNR. A blipped-CAIPI3 EPI trajectory modified for multi-shot acquisitions coupled with a multi-band RF pulse can simultaneously encode and acquire k-space data from multiple slice locations. However, the reconstruction of this data is extremely challenging. The images from the above acquisition will be not only slice aliased, but will exhibit severe artifacts due to inter-shot phase inconsistencies arising from the msDW encoding. Reconstruction of artifact-free DWIs from the above acquisition requires simultaneous phase compensation and slice unfolding. Existing methods depend on explicit4 or implicit5,6 navigators to calibrate the phase associated with each shot which is then used in a simultaneous slice-unfolding and phase-compensation reconstruction. We present a novel navigator-free reconstruction method, SMS MUSSELS, to achieve the above.
Methods
The proposed method exploits the low-rank property that exists between the multi-shot diffusion data. The MUSSELS7 formulation for the navigator-free reconstruction of msDW data proved the existence of annihilation relationships between multi-shot data of the form:
\begin{equation} \label{eq_8} {\bf{\cal H}}(\widehat{m_{i}})\cdot \widehat{\phi_j}[{\bf{k}}]- {\bf{\cal H}}(\widehat{m_{j}})\cdot\widehat{\phi_i}[{\bf{k}}]=0, \end{equation}
where $$$m_i(x), m_j(x)$$$ and $$$\phi_i(x), \phi_j(x)$$$ denote the DWI from shots $$$i, j$$$ and their phases respectively, $$$\widehat{m_i}[k], \widehat{m_j}[k],\widehat{\phi_i[k]}, \widehat{\phi_j[k]}$$$ denote the corresponding Fourier samples, and $$${\bf{\cal H}}$$$ represents the construction of the Hankel-structured convolution matrix. The existence of such linear relations assert that the block-Hankel matrix
\begin{equation}{\bf{H_1}}=[{\bf{\cal H}}(\widehat{m_{1}})\hspace{5mm}~{\bf{\cal H}}(\widehat{m_{2}}) \hspace{5mm}\cdots~\hspace{5mm}{\bf{\cal H}}(\widehat{m_{N_s}})],\end{equation}
formed out of the k-space data of each shots is rank-deficient. Here, $$$N_s$$$ denote the number of shots. In the SMS setting where $$$L$$$ slices are simultaneously excited, the above relation holds true independently for the shot data corresponding to each slice. Thus, we can state that
\begin{equation}{\bf{H}}_l=[{\bf{\cal H}}(\widehat{m_{1,l}})\hspace{5mm}~{\bf{\cal H}}(\widehat{m_{2,l}}) \hspace{5mm}\cdots\hspace{5mm}{\bf{\cal H}}(\widehat{m_{N_s,l}})];~~ l=1:L\end{equation}
is rank-deficient. We propose to make use of the above property to reconstruct the slice unaliased DWIs from the SMS-accelerated acquisition that are unaffected by phase artifacts. We pose the reconstruction of the slice unalised k-space data corresponding to each shot and each slice, $$${\bf{\widehat{m}}}$$$, as
\begin{equation}\label{use Hankel}\widehat{\tilde {\bf m}}= argmin_{{\bf{\widehat{m}}}} \underbrace{||{\mathcal{A}}\left({\bf{\widehat{m}}}\right)-{\bf{\widehat{y}}}||^2_{\ell_2}}_{\mbox{slice unfolding}} + \lambda\underbrace{\sum_{l=1}^{L}||{\bf H}_l({\bf{\widehat{{m}}}})||_*.}_{\mbox{low rank penalty}}\end{equation}
The operator $$${\mathcal{A}}\left({\bf{\widehat{m}}}\right)$$$ incorporates SMS slice folding and enforces data consistency with the measured k-space data, $$$\bf{\widehat y}$$$, of dimension $$$N_1\times N_2/N_s \times N_c\times N_{s}$$$. Here, $$$N_1\times N_2$$$ represents the size of the DWIs, and $$$N_c$$$ represents the number of channels. The different steps involved in the computation of $$${\mathcal A}\left({\bf{\widehat{m}}}\right)$$$ are illustrated in figure 1. The second term in eq. [4] enforces the low-rank property of the block-Hankel matrix for each slice by minimizing its nuclear norm. $$$ \lambda$$$ is a regularization parameter. The above cost function can be minimized using alternating minimization7 schemes that alternate between the data consistency term and the rank penalty term.
To test the proposed reconstruction, we collected diffusion data using a multi-shot blipped-CAIPI EPI sequence at various multi-shot and multi-band (MB) factors. A Stajeskal-Tanner sequence with b-value=700 s/mm2, 25 diffusion directions and one non-DWI was used for data acquisition using a 32 channel coil on 3T MRI. MB=2,3 and Ns=2,4 were tested. Other imaging parameters were: FOV= 210mm; slice thickness=2mm, NEX=1 with matrix sizes of 128x88 and 192x120. The proposed reconstructions were compared with SMS-MUSE6, another navigator-free reconstruction method.
Results
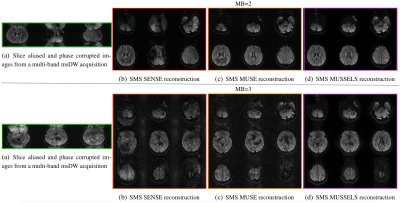
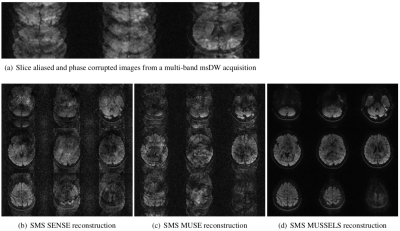
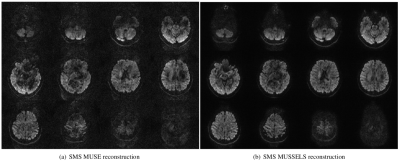
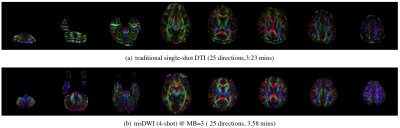
Figures 2-4 show the slice unfolded DWIs reconstructed using the proposed method at various multi-shot and multi-band factors. The reconstructed slice unfolded DWIs are free from phase artifacts even at high acceleration factors. In all cases, the proposed method shows significant improvement in image quality compared to the SMS-MUSE method. Figure 5 shows the color-coded fractional anisotropy (FA) maps derived from a tensor fit using all 25 DWIs reconstructed using the proposed method, which in comparison to a single-shot acquisition show drastic improvement in image quality.Conclusion
We proposed a new reconstruction method to simultaneously slice-unfold and jointly recover data from an SMS-accelerated msDW acquisition. We demonstrated the ability of SMS MUSSELS to effectively reconstruct 4-shot DW data accelerated using a multi-band factor of 3. The 3x improved time-efficiency via this SMS-acceleration enables the practical application of multishot acquisitions in high angular resolution diffusion studies.Acknowledgements
No acknowledgement found.References
1. Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, and Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. Journal of Magnetic Resonance Imaging, 2001.
2. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, and Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magnetic Resonance in Medicine, 2005.
3. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, and Wald LL. Blipped-controlled aliasing in par- allel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magnetic Resonance in Medicine, 2012.
4. Dai E, Ma X, Zhang Z, Yuan C, and Guo H. Simultaneous multislice accelerated interleaved EPI DWI using generalized blipped-CAIPI acquisition and 3D K-space reconstruction. Magnetic Resonance in Medicine, 2017.
5. Hashemizadehkolowri S, Chen RR, Dibella E, Hsu E, Ying L, and Adluru G. Improving image reconstructions for simultaneous multi-slice readout-segmented diffusion MRI data with phase errors. In Proceedings - International Symposium on Biomedical Imaging, 2018. ISBN 9781538636367.
6. Herbst M, Deng W, Ernst T, and Stenger VA. Segmented simultaneous multi-slice diffusion weighted imaging with generalized trajectories. Magnetic Resonance in Medicine, 2017.
7. Mani, M., Jacob, M., Kelley, D. and Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. doi: 10.1002/mrm.26382, 2016
Figures